Table of Contents
The Stochastic Survivable Network Design Problem
This page contains further informations and benchmark data for the Stochastic Survivable Network Design Problem (SSNDP) and our work on this topic:
- Stochastic Survivable Network Design Problems: Theory and practice
Ivana Ljubic, Petra Mutzel, and Bernd Zey
European Journal of Operational Research (EJOR), volume 256, issue 2, 2017, pp. 333-348 - Stochastic Survivable Network Design Problems
Ivana Ljubic, Petra Mutzel, and Bernd Zey
International Network Optimization Conference (INOC)
Electronic Notes in Discrete Mathematics (ENDM), 2013, pp.245-252
or the related technical report
- Stochastic Survivable Network Design Problems
Ivana Ljubic, Petra Mutzel, and Bernd Zey, algorithm engineering report TR12-1-003, 2012. Visit our stoch. network design webpage for further informations
Problem Definition
The deterministic survivable network design problem (NDP) is defined as follows:
Given is an undirected graph 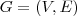 , edge costs
, edge costs 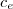 , and a
, and a 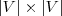 matrix
matrix  defining the edge connectivity requirements.
The objective consists of finding a set of edges
defining the edge connectivity requirements.
The objective consists of finding a set of edges  such that there exist at least
such that there exist at least 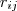 edge disjoint path between vertice
edge disjoint path between vertice  and
and 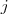 ,
, 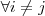 , with minimum costs, i.e.,
, with minimum costs, i.e., 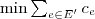 .
.
Here, we consider the two-stage stochastic survivable network design problem (SSNDP) with fixed recourse and finitely many scenarios in which the edge requirements and the edge costs are subject to uncertainty. This means there are two points in times (also called stages): In the first stage (now, on Monday), we only have probabilistic information in terms of possible outcomes (scenarios) in the future (second stage, on Tuesday).
A scenario 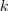 thereby specifies edge requirements
thereby specifies edge requirements 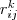 , edge costs
, edge costs 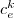 , and a probability
, and a probability 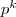 for it to be realized. Expected edge costs in the second stage are higher and based on these informations, we may buy some edges at a lower price now and in the second stage, when one of the given scenarios is realized, we have to purchase additional edges in order to satisfy the connectivity requirements.
for it to be realized. Expected edge costs in the second stage are higher and based on these informations, we may buy some edges at a lower price now and in the second stage, when one of the given scenarios is realized, we have to purchase additional edges in order to satisfy the connectivity requirements.
The goal is to make a decision about edges to be purchased in the first stage while minimizing the expected cost of the full solution (i.e., after the second stage).
More formally, let 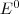 be the selected first-stage edges and
be the selected first-stage edges and 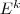 the edges of the
the edges of the 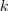 th scenario.
Then the objective is
th scenario.
Then the objective is 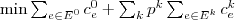 .
.
Instances
Generation
Deterministic instances were generated by adopting the idea of Johnson, Minkoff, and Phillips (D. S. Johnson, M. Minkoff, and S. Phillips. The prize-collecting Steiner tree problem: Theory and practice. In ACM-SIAM SODA, pages 760-–769. SIAM, 2000), for the prize-collecting Steiner tree problem,
which is frequently used as benchmark in the network design community.
After randomly distributing 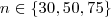 points in the unit square, a minimum spanning tree is computed using the points as nodes and the Euclidean distances between all vertex pairs as edge costs.
To generate only feasible instances we augmented this tree by inserting edges between leaves which are adjacent in the planar embedding.
points in the unit square, a minimum spanning tree is computed using the points as nodes and the Euclidean distances between all vertex pairs as edge costs.
To generate only feasible instances we augmented this tree by inserting edges between leaves which are adjacent in the planar embedding.
The resulting biconnected graph is extended by adding all edges for which the Euclidean distance is less than or equal to 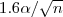 .
We have introduced
.
We have introduced  in order to control the density of the graph. (The original parameter used by Johnson, Minkoff, and Phillips was
in order to control the density of the graph. (The original parameter used by Johnson, Minkoff, and Phillips was 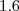 and corresponds to
and corresponds to 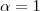 in our setting).
In our experiments we use
in our setting).
In our experiments we use 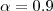 which led to graphs with average density
which led to graphs with average density 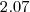 .
The edge-connectivity requirements are set as follows.
We have randomly drawn
.
The edge-connectivity requirements are set as follows.
We have randomly drawn 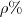 of the nodes as base sets of
of the nodes as base sets of  and
and  customers.
Here, we use
customers.
Here, we use 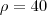 and we additionally introduce a random root node that is contained in
and we additionally introduce a random root node that is contained in  .
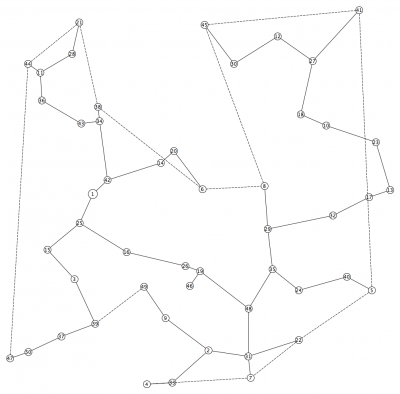
An example is given in Figures below.
.
An example is given in Figures below.
To transform these instances into stochastic ones we randomly and independently generate 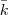 scenarios.
The probabilities are set by randomly distributing
scenarios.
The probabilities are set by randomly distributing 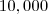 points over the scenarios, where
each point corresponds to a probability of
points over the scenarios, where
each point corresponds to a probability of 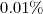 .
Edge costs
.
Edge costs 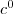 in the first stage are Euclidean distances and in the second stage
for each edge
in the first stage are Euclidean distances and in the second stage
for each edge  and scenario
and scenario 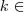 randomly drawn from the interval
randomly drawn from the interval ![Math $[1.1c_e^0, 1.3c_e^0]$](/lib/exe/fetch.php?media=wiki:latex:/img2c6fea82b0ffcc4741a17f938c1494b4.png) .
Edge-connectivity requirements are generated by randomly drawing
.
Edge-connectivity requirements are generated by randomly drawing 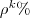 from the vertex sets
from the vertex sets  and
and  each as
each as 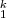 and
and 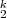 customers, respectively, for scenario
customers, respectively, for scenario 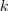 .
Here, we use
.
Here, we use 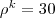 for all scenarios
for all scenarios 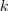 .
The special root node was set to be an
.
The special root node was set to be an 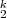 node in each scenario
node in each scenario 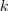 .
.
For each deterministic instance we generated a stochastic instance with 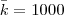 scenarios
and took the first
scenarios
and took the first 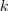 to obtain an SSNDP instance for
to obtain an SSNDP instance for
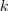 scenarios\footnote; We used 14 values for
scenarios\footnote; We used 14 values for 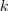 :
: 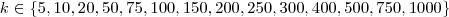 .
Probabilities for the scenarios of the instances with
.
Probabilities for the scenarios of the instances with 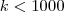 are scaled appropriately.
Overall, we generated 20 graphs for each
are scaled appropriately.
Overall, we generated 20 graphs for each 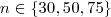 and
and 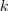 leading to
840 instances which can be downloaded in the Download section.
leading to
840 instances which can be downloaded in the Download section.
File format
Each file has the same structure and consists of 5 important parts
- general: number of scenarios and id of the root node (if there is a root node)
- probabilities: the probabilities for each scenario which should sum up to 1
- node: each line represents a node with the following informations:
- identifier (normally starts at 1)
- x- and y-coordinate (for drawing purposes only)
- link: each line represents an edge with the following informations:
- identifier (normally starts at 1)
- identifier of the source and target node
- a (
 )-vector with the weights for this edge in the first stage and each scenario
)-vector with the weights for this edge in the first stage and each scenario
- connectivity: each line contains the list of nodes in
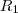 or
or 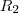 , respectively, for each scenario:
, respectively, for each scenario:- scenario id (normally starts at 0 (not consistent with other ids - sorry!)
- 1 (x)or 2: indicates wether the list of nodes are
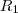 or
or 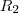 nodes
nodes - the size of
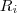
- the list of the
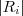 vertices
vertices
All values are separated by a tabulator (“\t”).
Lines starting with a “#” are comments. In general, each file starts with some informations about the deterministic instance, the probability distribution, etc.
Example:
# automatically generated file (type G) # (type G: random points in unit square + MST + edge=(i,j) iff distance(i,j) < alpha/sqrt(n)) # 20 nodes, 44 edges # parameters: # alpha=0.90000 # nr Scenarios=5 # distribution=equal # probability(R2)=42, probability(R1)=41 # scenario-probability(R2)=32, scenario-probability(R1)=31 # edge-costs in [1.1000c_e, 1.3000c_e] general # nr scenarios | root node (if given) 5 1 probabilities # probability for each scenario (p_k) 0.15310 0.23660 0.20280 0.21270 0.19480 node #id x y 1 745.01 619.98 2 703.93 329.02 3 631.63 468.01 <etc.> link # id | source | target | weight 1st stage | weight Scenario 1 | weight Scenario 2 | ... 1 1 2 293.00 327.00 365.00 362.00 327.00 370.00 2 1 3 189.00 236.00 230.00 215.00 218.00 217.00 <etc.> connectivity #scenario R_1 or R_2 |R_i| list of nodes in R_i 0 1 3 11 13 18 0 2 2 1 2 1 1 2 15 16 1 2 2 1 6 2 1 3 10 12 16 2 2 2 1 5
Downloads
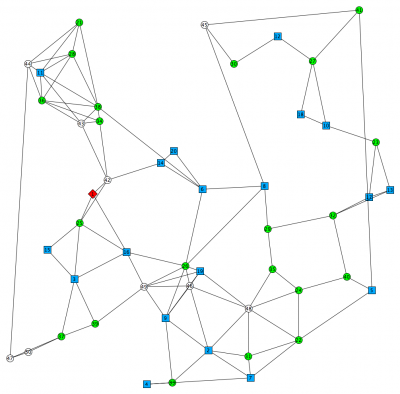
- The red vertex is the root node which is an
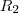 -node in each scenario. The green and blue vertices are potential
-node in each scenario. The green and blue vertices are potential 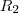 and
and 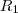 vertices, respectively.
vertices, respectively.
Results
Some results (5 out of 20 instances) for the 50-vertices instances can be found in the following table.
| instance | 2-stage branch&cut | 2-stage branch&cut (Magnanti-Wong) | 2-stage branch&cut (strengthened cuts) | Deterministic Equivalent | ||||||||||||||||||||||
| name | e | K | OPT | UB | t[s] | iter. Master | b&b | LP root | gap | UB | t[s] | iter. Master | b&b | LP root | gap | UB | t[s] | iter. Master | b&b | LP root | gap | UB | t[s] | b&b | LP root | gap |
| g-50-103-19-22-0.75–30-30–10-30–5s.ssndp | 103 | 5 | 4658,94 | 4658,94 | 7,064 | 114 | 1 | 4658,94 | 0 | 4658,94 | 2,422 | 26,6 | 1 | 4658,94 | 0 | 4658,94 | 1,308 | 36 | 1 | 4658,94 | 0 | 4658,94 | 0,234 | 1 | 4658,94 | 0 |
| g-50-103-19-22-0.75–30-30–10-30–10s.ssndp | 103 | 10 | 4866,08 | 4866,08 | 42,718 | 101 | 41 | 4861,02 | <0,01 | 4866,08 | 17,114 | 23,6 | 37,8 | 4861,02 | <0,01 | 4866,08 | 8,944 | 33 | 43 | 4861,02 | <0,01 | 4866,08 | 1,348 | 3 | 4861,02 | <0,01 |
| g-50-103-19-22-0.75–30-30–10-30–20s.ssndp | 103 | 20 | 4747,74 | 4747,74 | 38,346 | 69 | 11 | 4738,26 | <0,01 | 4747,74 | 16,768 | 19,6 | 11 | 4738,26 | <0,01 | 4747,74 | 9,072 | 26 | 11 | 4738,26 | <0,01 | 4747,74 | 14,45 | 27 | 4738,26 | <0,01 |
| g-50-103-19-22-0.75–30-30–10-30–50s.ssndp | 103 | 50 | 4602,32 | 4602,32 | 115,774 | 54 | 17 | 4594,94 | <0,01 | 4602,32 | 55,308 | 16,2 | 17 | 4594,94 | <0,01 | 4602,32 | 33,67 | 23 | 17 | 4594,94 | <0,01 | 4602,32 | 206,026 | 69 | 4594,94 | <0,01 |
| g-50-103-19-22-0.75–30-30–10-30–75s.ssndp | 103 | 75 | 4593,5 | 4593,5 | 75,51 | 51 | 7 | 4589,94 | <0,01 | 4593,5 | 51,182 | 17,8 | 7 | 4589,94 | <0,01 | 4593,5 | 24,222 | 22 | 7 | 4589,94 | <0,01 | 4593,5 | 876,948 | 183 | 4589,94 | <0,01 |
| g-50-103-19-22-0.75–30-30–10-30–100s.ssndp | 103 | 100 | 4609,85 | 4609,85 | 160,988 | 43 | 9 | 4608,01 | <0,01 | 4609,85 | 71,242 | 16,4 | 9 | 4608,01 | <0,01 | 4609,85 | 36,578 | 20 | 9 | 4608,01 | <0,01 | 4609,85 | 7200 | 1043 | 4608,01 | <0,01 |
| g-50-103-19-22-0.75–30-30–10-30–150s.ssndp | 103 | 150 | 4600,04 | 4600,04 | 240,868 | 38 | 7 | 4597,76 | <0,01 | 4600,04 | 108,454 | 14 | 7 | 4597,76 | <0,01 | 4600,04 | 94,458 | 18 | 7 | 4597,76 | <0,01 | - | 7200 | 367,4 | 4597,76 | - |
| g-50-103-19-22-0.75–30-30–10-30–200s.ssndp | 103 | 200 | 4607,58 | 4607,58 | 358,342 | 34 | 13 | 4605,18 | <0,01 | 4607,58 | 193,274 | 14,4 | 13 | 4605,18 | <0,01 | 4607,58 | 127,816 | 16 | 13 | 4605,18 | <0,01 | - | 7200 | 138,2 | 4605,18 | - |
| g-50-103-19-22-0.75–30-30–10-30–250s.ssndp | 103 | 250 | 4642,6 | 4642,6 | 365,134 | 36 | 11 | 4639,57 | <0,01 | 4642,6 | 246,268 | 13,8 | 11 | 4639,57 | <0,01 | 4642,6 | 115,438 | 17 | 11 | 4639,57 | <0,01 | - | 7200 | 77,4 | 4639,57 | - |
| g-50-105-16-27-0.75–30-30–10-30–5s.ssndp | 105 | 5 | 4486,62 | 4486,62 | 8,478 | 137 | 1 | 4486,62 | 0 | 4486,62 | 3,904 | 38,8 | 1 | 4486,62 | 0 | 4486,62 | 2,288 | 53 | 1 | 4486,62 | 0 | 4486,62 | 0,358 | 1 | 4486,62 | 0 |
| g-50-105-16-27-0.75–30-30–10-30–10s.ssndp | 105 | 10 | 4408,82 | 4408,82 | 11,094 | 84 | 3 | 4408,35 | <0,01 | 4408,82 | 5,47 | 25 | 3 | 4408,35 | <0,01 | 4408,82 | 2,988 | 33 | 3 | 4408,35 | <0,01 | 4408,83 | 1,638 | 3 | 4408,35 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–20s.ssndp | 105 | 20 | 4660,71 | 4660,71 | 28,224 | 66 | 11 | 4658,71 | <0,01 | 4660,71 | 17,738 | 22,4 | 11 | 4658,71 | <0,01 | 4660,71 | 9,21 | 30 | 11 | 4658,71 | <0,01 | 4660,71 | 14,46 | 15 | 4658,71 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–50s.ssndp | 105 | 50 | 4621,09 | 4621,09 | 35,4 | 43 | 5 | 4619,11 | <0,01 | 4621,09 | 20,37 | 14 | 5 | 4619,11 | <0,01 | 4621,09 | 11,054 | 17 | 5 | 4619,11 | <0,01 | 4621,09 | 147,772 | 41 | 4619,11 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–75s.ssndp | 105 | 75 | 4598,97 | 4598,97 | 53,87 | 42 | 9 | 4598,37 | <0,01 | 4598,97 | 41,778 | 15,8 | 9 | 4598,37 | <0,01 | 4598,97 | 21,254 | 21 | 9 | 4598,37 | <0,01 | 4598,97 | 115,132 | 9 | 4598,37 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–100s.ssndp | 105 | 100 | 4607,8 | 4607,8 | 72,658 | 40 | 5 | 4606,4 | <0,01 | 4607,8 | 48,806 | 14,6 | 5 | 4606,4 | <0,01 | 4607,8 | 22,38 | 16 | 5 | 4606,4 | <0,01 | 4607,8 | 902,77 | 71 | 4606,4 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–150s.ssndp | 105 | 150 | 4729,89 | 4729,89 | 93,424 | 38 | 3 | 4729,39 | <0,01 | 4729,89 | 57,404 | 14,8 | 3 | 4729,39 | <0,01 | 4729,89 | 33,09 | 17 | 3 | 4729,39 | <0,01 | 4729,89 | 513,1 | 5 | 4729,39 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–200s.ssndp | 105 | 200 | 4727,6 | 4727,6 | 127,312 | 37 | 3 | 4727,1 | <0,01 | 4727,6 | 79,582 | 15 | 3 | 4727,1 | <0,01 | 4727,6 | 42,366 | 17 | 3 | 4727,1 | <0,01 | 4727,6 | 1301,144 | 3 | 4727,1 | <0,01 |
| g-50-105-16-27-0.75–30-30–10-30–250s.ssndp | 105 | 250 | 4745,26 | 4745,26 | 168,654 | 37 | 3 | 4745,02 | <0,01 | 4745,26 | 101,922 | 14,8 | 3 | 4745,02 | <0,01 | 4745,26 | 53,198 | 17 | 3 | 4745,02 | <0,01 | 4745,26 | 2399,21 | 3 | 4745,02 | <0,01 |
| g-50-110-29-14-0.75–30-30–10-30–5s.ssndp | 110 | 5 | 3970,78 | 3970,78 | 8,722 | 123 | 1 | 3970,78 | 0 | 3970,78 | 3,444 | 34,8 | 1 | 3970,78 | 0 | 3970,78 | 1,756 | 41 | 1 | 3970,78 | 0 | 3970,78 | 0,21 | 1 | 3970,78 | 0 |
| g-50-110-29-14-0.75–30-30–10-30–10s.ssndp | 110 | 10 | 4022,78 | 4022,78 | 12,836 | 93 | 1 | 4022,78 | 0 | 4022,78 | 4,012 | 21,8 | 1 | 4022,78 | 0 | 4022,78 | 1,918 | 25 | 1 | 4022,78 | 0 | 4022,78 | 0,848 | 1 | 4022,78 | 0 |
| g-50-110-29-14-0.75–30-30–10-30–20s.ssndp | 110 | 20 | 4354,77 | 4354,77 | 42,324 | 82 | 11 | 4349,91 | <0,01 | 4354,77 | 21,728 | 28,2 | 11 | 4349,91 | <0,01 | 4354,77 | 10,02 | 31 | 11 | 4349,91 | <0,01 | 4354,77 | 8,55 | 5 | 4349,91 | <0,01 |
| g-50-110-29-14-0.75–30-30–10-30–50s.ssndp | 110 | 50 | 4143,13 | 4143,13 | 48,31 | 50 | 5 | 4138,57 | <0,01 | 4143,13 | 26,608 | 16,2 | 5 | 4138,57 | <0,01 | 4143,13 | 11,57 | 18 | 5 | 4138,57 | <0,01 | 4143,13 | 34,492 | 5 | 4138,57 | <0,01 |
| g-50-110-29-14-0.75–30-30–10-30–75s.ssndp | 110 | 75 | 4128,37 | 4128,37 | 62,81 | 49 | 3 | 4127,13 | <0,01 | 4128,37 | 30,598 | 16,8 | 3 | 4127,13 | <0,01 | 4128,37 | 15,042 | 19 | 3 | 4127,13 | <0,01 | 4128,37 | 1652,282 | 271 | 4127,13 | <0,01 |
| g-50-110-29-14-0.75–30-30–10-30–100s.ssndp | 110 | 100 | 4117,53 | 4117,53 | 97,232 | 45 | 5 | 4112,51 | <0,01 | 4117,53 | 47,468 | 14,4 | 5 | 4112,51 | <0,01 | 4117,53 | 22,99 | 17 | 5 | 4112,51 | <0,01 | 4117,53 | 5414,596 | 489 | 4112,51 | <0,01 |
| g-50-110-29-14-0.75–30-30–10-30–150s.ssndp | 110 | 150 | 4122,87 | 4122,87 | 142,188 | 43 | 5 | 4118,6 | <0,01 | 4122,87 | 73,892 | 14,6 | 5 | 4118,6 | <0,01 | 4122,87 | 35,016 | 17 | 5 | 4118,6 | <0,01 | - | 7200 | 325,4 | 4118,6 | - |
| g-50-110-29-14-0.75–30-30–10-30–200s.ssndp | 110 | 200 | 4129,47 | 4129,47 | 234,138 | 39 | 9 | 4121,33 | <0,01 | 4129,47 | 139,302 | 14 | 9 | 4121,33 | <0,01 | 4129,47 | 62,792 | 16 | 9 | 4121,33 | <0,01 | - | 7200 | 117,4 | 4121,33 | - |
| g-50-110-29-14-0.75–30-30–10-30–250s.ssndp | 110 | 250 | 4145,47 | 4145,47 | 283,398 | 38 | 7 | 4138,25 | <0,01 | 4145,47 | 169,334 | 14,2 | 7 | 4138,25 | <0,01 | 4145,47 | 72,032 | 16 | 7 | 4138,25 | <0,01 | - | 7200 | 75,4 | 4138,25 | - |
| g-50-119-16-23-0.75–30-30–10-30–5s.ssndp | 119 | 5 | 4728,91 | 4728,91 | 14,518 | 136 | 3 | 4728,51 | <0,01 | 4728,91 | 4,732 | 31,2 | 3 | 4728,51 | <0,01 | 4728,91 | 3,216 | 44 | 3 | 4728,51 | <0,01 | 4728,91 | 0,554 | 3 | 4728,51 | <0,01 |
| g-50-119-16-23-0.75–30-30–10-30–10s.ssndp | 119 | 10 | 4744,97 | 4744,97 | 52,35 | 240 | 11 | 4694,43 | 0,011 | 4744,97 | 34,35 | 35,6 | 11 | 4694,43 | 0,011 | 4744,97 | 17,062 | 43 | 11 | 4694,43 | 0,011 | 4744,97 | 13,45 | 25 | 4694,43 | 0,011 |
| g-50-119-16-23-0.75–30-30–10-30–20s.ssndp | 119 | 20 | 4758,29 | 4758,29 | 59,89 | 80 | 15 | 4739,47 | <0,01 | 4758,29 | 34,724 | 26,4 | 15 | 4739,47 | <0,01 | 4758,29 | 17,096 | 34 | 15 | 4739,47 | <0,01 | 4758,29 | 46,822 | 31 | 4739,47 | <0,01 |
| g-50-119-16-23-0.75–30-30–10-30–50s.ssndp | 119 | 50 | 4827,79 | 4827,79 | 90,432 | 53 | 3 | 4826,49 | <0,01 | 4827,79 | 33,918 | 18 | 3 | 4826,49 | <0,01 | 4827,79 | 23,418 | 23 | 3 | 4826,49 | <0,01 | 4827,79 | 204,652 | 19 | 4826,49 | <0,01 |
| g-50-119-16-23-0.75–30-30–10-30–75s.ssndp | 119 | 75 | 4868,24 | 4868,24 | 121,174 | 46 | 7 | 4859,7 | <0,01 | 4868,24 | 65,592 | 16,8 | 7 | 4859,7 | <0,01 | 4868,24 | 37,542 | 18 | 7 | 4859,7 | <0,01 | 4868,24 | 945,546 | 59 | 4859,7 | <0,01 |
| g-50-119-16-23-0.75–30-30–10-30–100s.ssndp | 119 | 100 | 4870,24 | 4870,24 | 157,236 | 44 | 7 | 4864,13 | <0,01 | 4870,24 | 95,2 | 16,4 | 7 | 4864,13 | <0,01 | 4870,24 | 52,23 | 20 | 7 | 4864,13 | <0,01 | 4870,24 | 3435,446 | 181 | 4864,13 | <0,01 |
| g-50-119-16-23-0.75–30-30–10-30–150s.ssndp | 119 | 150 | 4916,18 | 4916,18 | 268,31 | 43 | 5 | 4910,75 | <0,01 | 4916,18 | 153,51 | 14,8 | 5 | 4910,75 | <0,01 | 4916,18 | 77,678 | 17 | 5 | 4910,75 | <0,01 | - | 7200 | 178,2 | 4910,75 | - |
| g-50-119-16-23-0.75–30-30–10-30–200s.ssndp | 119 | 200 | 4899,86 | 4899,86 | 283,988 | 41 | 3 | 4898,57 | <0,01 | 4899,86 | 132,49 | 14,8 | 3 | 4898,57 | <0,01 | 4899,86 | 77,676 | 16 | 3 | 4898,57 | <0,01 | - | 7200 | 25 | 4898,57 | - |
| g-50-119-16-23-0.75–30-30–10-30–250s.ssndp | 119 | 250 | 4907,03 | 4907,03 | 615,02 | 38 | 5 | 4905,16 | <0,01 | 4907,03 | 222,066 | 14 | 3 | 4905,16 | <0,01 | 4907,03 | 115,342 | 16 | 3 | 4905,16 | <0,01 | - | 7200 | 1 | - | - |
| g-50-123-24-18-0.75–30-30–10-30–5s.ssndp | 123 | 5 | 5159,49 | 5159,49 | 31,314 | 328 | 9 | 5149,51 | <0,01 | 5159,49 | 12,072 | 57,2 | 10,2 | 5149,51 | <0,01 | 5159,49 | 6,408 | 77 | 9 | 5149,51 | <0,01 | 5159,49 | 1,538 | 13 | 5149,51 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–10s.ssndp | 123 | 10 | 4794,93 | 4794,93 | 25,124 | 121 | 7 | 4790,5 | <0,01 | 4794,93 | 10,852 | 28,2 | 7 | 4790,5 | <0,01 | 4794,93 | 5,23 | 35 | 7 | 4790,5 | <0,01 | 4794,93 | 2,726 | 7 | 4790,5 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–20s.ssndp | 123 | 20 | 4977,58 | 4977,58 | 70,04 | 181 | 11 | 4969,57 | <0,01 | 4977,58 | 29,864 | 26,8 | 11 | 4969,57 | <0,01 | 4977,58 | 15,998 | 31 | 11 | 4969,57 | <0,01 | 4977,58 | 98,436 | 101 | 4969,57 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–50s.ssndp | 123 | 50 | 4862,66 | 4862,66 | 325,148 | 271 | 31 | 4858,03 | <0,01 | 4862,66 | 103,666 | 21,2 | 29 | 4858,03 | <0,01 | 4862,66 | 43,82 | 23 | 29 | 4858,03 | <0,01 | 4862,66 | 2954,048 | 691 | 4858,03 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–75s.ssndp | 123 | 75 | 4775,09 | 4775,09 | 166,21 | 101 | 11 | 4773,38 | <0,01 | 4775,09 | 81,668 | 19,4 | 12,6 | 4773,38 | <0,01 | 4775,09 | 36,086 | 22 | 11 | 4773,38 | <0,01 | 4775,09 | 2501,89 | 271 | 4773,38 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–100s.ssndp | 123 | 100 | 4798,76 | 4798,76 | 161,248 | 52 | 5 | 4797,8 | <0,01 | 4798,76 | 63,788 | 17,6 | 5 | 4797,8 | <0,01 | 4798,76 | 46,89 | 18 | 5 | 4797,8 | <0,01 | 4798,76 | 7091,142 | 359 | 4797,8 | <0,01 |
| g-50-123-24-18-0.75–30-30–10-30–150s.ssndp | 123 | 150 | 4879,05 | 4879,05 | 1076,024 | 195 | 17 | 4875,8 | <0,01 | 4879,05 | 202,584 | 17,2 | 15 | 4875,8 | <0,01 | 4879,05 | 85,064 | 20 | 17 | 4875,8 | <0,01 | - | 7200 | 188,2 | 4875,8 | - |
| g-50-123-24-18-0.75–30-30–10-30–200s.ssndp | 123 | 200 | 4893,47 | 4893,47 | 876,916 | 49 | 19 | 4889,36 | <0,01 | 4893,47 | 323,776 | 17 | 15,8 | 4889,36 | <0,01 | 4893,47 | 131,936 | 18 | 19 | 4889,36 | <0,01 | - | 7200 | 61,4 | 4889,36 | - |
| g-50-123-24-18-0.75–30-30–10-30–250s.ssndp | 123 | 250 | 4860,85 | 4860,85 | 1500,892 | 101 | 19 | 4858,03 | <0,01 | 4860,85 | 427,466 | 16,8 | 17 | 4858,03 | <0,01 | 4860,85 | 140,812 | 19 | 15 | 4858,03 | <0,01 | - | 7200 | 21,4 | 4858,03 | - |
description:
- e: the number of edges
- OPT: the optimum solution
- UB: best found solution (Upper Bound)
- t[s]: the running time in seconds
- b&b: the number of branch&bound nodes
- LP root: lp-value of the problem in the root node
- gap = (UB-LP)/UB
- iter. Master: iterations of the master in the 2-stage branch&cut algorithm
Example
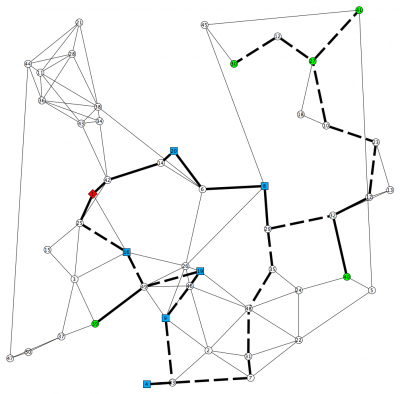
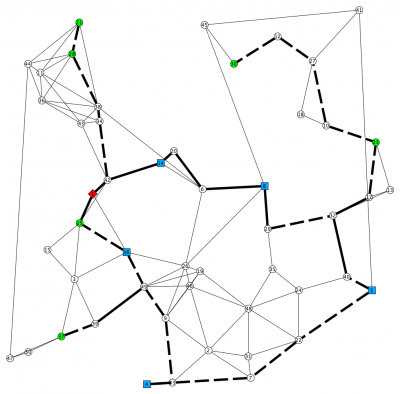
Below one can see two scenarios of an optimum solution of an instance with 50 vertices and 5 scenarios
(g-50-101-5scenarios).
The solid lines are the edges bought in the first stage, the dashed lines depict the edges of the scenario. The red vertex is the root node, the green vertices are 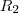 and the blue vertices
and the blue vertices 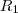 nodes, respectively, of the scenario.
nodes, respectively, of the scenario.
As one can easily see, the first stage is disconnected.
The images are generated by storing the solution as .gml file, loading it with yEd, and exporting it as a .png.