`continuous` — Real-valued Test Problems¶

This module contains miscellaneous test problems with continuous/real-valued search space. The problems are mostly from the early days of research on optimization.

Dixon-Szegö Collection¶

The collection by Dixon and Szegö contains seven multimodal problems. All are non-separable, but otherwise quite easy.

Class name	Problem name	Number variables	Global optima	Local optima
`optproblems.continuous.Shekel`	Shekel5	4	1	5
`optproblems.continuous.Shekel`	Shekel7	4	1	7
`optproblems.continuous.Shekel`	Shekel10	4	1	10
`optproblems.continuous.Hartman3`	Hartman3	3	1	3
`optproblems.continuous.Hartman6`	Hartman6	6	1	2
`optproblems.continuous.Branin`	Branin	2	3	3
`optproblems.continuous.GoldsteinPrice`	GoldsteinPrice	2	1	4

class optproblems.continuous.DixonSzegoe(**kwargs)¶

The test problem collection of Dixon and Szegoe for global optimization.

This class inherits from list and fills itself with the seven problems Shekel5, Shekel7, Shekel10, Hartman3, Hartman6, Branin, and GoldsteinPrice. The arguments to the constructor are passed through to the problem classes.

References

[Dixon1978]

(1, 2, 3) L.C.W. Dixon and G.P. Szegoe, The global optimization problem: an introduction, pp. 1-15 in: in L.C.W. Dixon and G.P. Szegoe (eds.), Towards Global Optimisation 2, North-Holland, Amsterdam 1978.

class optproblems.continuous.Shekel(num_optima, phenome_preprocessor=None, **kwargs)¶

Shekel’s family of test problems.

As defined in [Dixon1978]. The problems have four variables with lower and upper bounds of 0 and 10, respectively.

__init__(num_optima, phenome_preprocessor=None, **kwargs)¶

Constructor.

Parameters:	num_optima (int) – The number of local optima. Must be between 1 and 10. kwargs – Arbitrary keyword arguments, passed through to the constructor of the super class.

get_locally_optimal_solutions(max_number=None)¶

Return locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.Hartman3(phenome_preprocessor=None, **kwargs)¶

A 3-D instance of Hartman’s family.

The principle for defining problems of this family was presented in [Hartman1972]. The numbers for this instance can be found in [Dixon1978]. The search space is the unit hypercube.

References

[Hartman1972]

(1, 2) Hartman, James K. (1972). Some Experiments in Global Optimization. Technical report NP5 55HH72051A, Naval Postgraduate School, Monterey, California.

get_locally_optimal_solutions(max_number=None)¶

Return locally optimal solutions.

According to [Toern1999], this problem has four local optima. However, only three could be found experimentally.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

References

[Toern1999]

(1, 2) A. Toern; M.M. Ali; S. Viitanen (1999). Stochastic Global Optimization: Problem Classes and Solution Techniques. Journal of Global Optimization, vol. 14, pp. 437-447.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.Hartman6(phenome_preprocessor=None, **kwargs)¶

A 6-D instance of Hartman’s family.

The principle for defining problems of this family was presented in [Hartman1972]. The numbers for this instance can be found in [Dixon1978]. The search space is the unit hypercube.

get_locally_optimal_solutions(max_number=None)¶

Return locally optimal solutions.

According to [Toern1999], this problem has four local optima. However, only two could be found experimentally.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.branin(phenome)¶: The bare-bones Branin function.

class optproblems.continuous.Branin(phenome_preprocessor=None, **kwargs)¶

Branin’s test problem ‘RCOS’.

The search space is $[-5, 0] \times [10, 15]$ . Every optimum is a global optimum.

get_locally_optimal_solutions(max_number=None)¶: Return the three global optima.

get_optimal_solutions(max_number=None)¶: Return the three global optima.

optproblems.continuous.goldstein_price(phenome)¶: The bare-bones Goldstein-Price function.

class optproblems.continuous.GoldsteinPrice(phenome_preprocessor=None, **kwargs)¶

A test problem by Goldstein and Price.

The search space is $[-2, 2] \times [-2, 2]$ .

get_locally_optimal_solutions(max_number=None)¶

Return the four locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

Other Problems¶

The following table gives an overview of the other test problems in this module. Where it is not necessary by the implementation, bound constraints are not given. However, constraints can of course be defined by the user. The last two columns give the numbers of optima positions. In the column with local optima, exp means that the number is exponential in n, but the exact value depends on the bounds. The positions of local optima can only be obtained for those problems in the table where an exact number of local optima is given (with the exception of FletcherPowell). For Schaffer6 and Schaffer7, the optima positions are not discrete.

Class/Problem name	Number variables	Bound-constrained	Global optima	Local optima
`optproblems.continuous.Ackley`	n	no	1	exp
`optproblems.continuous.DoubleSum`	n	no	1	1
`optproblems.continuous.Ellipsoid`	n	no	1	1
`optproblems.continuous.FletcherPowell`	n	yes	1	2^n
`optproblems.continuous.Griewank`	n	no	1	exp
`optproblems.continuous.Himmelblau`	2	no	4	4
`optproblems.continuous.LunacekTwoSpheres`	n	yes	1	2
`optproblems.continuous.LunacekTwoRastrigins`	n	yes	1	exp
`optproblems.continuous.ModifiedRastrigin`	4, 8, 16	yes	1	48
`optproblems.continuous.Rastrigin`	n	no	1	exp
`optproblems.continuous.Rosenbrock`	n	no	1	?
`optproblems.continuous.Schaffer6`	2	yes	1	inf
`optproblems.continuous.Schaffer7`	2	yes	1	inf
`optproblems.continuous.Schwefel`	n	yes	1	7^n
`optproblems.continuous.SixHumpCamelback`	2	no	2	6
`optproblems.continuous.Sphere`	n	no	1	1
`optproblems.continuous.Vincent`	n	yes	6^n	6^n
`optproblems.continuous.Weierstrass`	n	no	1	exp

optproblems.continuous.ackley(phenome)¶: The bare-bones Ackley function.

class optproblems.continuous.Ackley(num_variables=10, phenome_preprocessor=None, **kwargs)¶

Ackley’s test problem.

No bound constraints are pre-defined for this problem.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.double_sum(phenome)¶: Schwefel’s problem 1.2

class optproblems.continuous.DoubleSum(num_variables=30, phenome_preprocessor=None, **kwargs)¶

Schwefel’s double-sum problem.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.EllipsoidFunction(a=1000000.0)¶

A configurable Ellipsoid function.

The basic one-dimensional formula reads a ** exponent * x ** 2.

class optproblems.continuous.Ellipsoid(num_variables=30, a=1000000.0, phenome_preprocessor=None, **kwargs)¶

A configurable ellipsoidal test problem.

No bound constraints are pre-defined for this problem.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.FletcherPowell(num_variables=10, rand_gen=None, phenome_preprocessor=None, **kwargs)¶

Fletcher and Powell’s test problem.

Each decision variable is restricted to $[-\pi, \pi]$ and the search space is periodic.

References

[Fletcher1963]

R. Fletcher and M. J. D. Powell (1963). A Rapidly Convergent Descent Method for Minimization. The Computer Journal 6(2): 163-168, https://dx.doi.org/10.1093/comjnl/6.2.163

__init__(num_variables=10, rand_gen=None, phenome_preprocessor=None, **kwargs)¶

Constructor.

Parameters:

num_variables (int, optional) – The number of decision variables.
rand_gen (random.Random, optional) – A generator for random numbers. If omitted, the global instance of the module random is used.
phenome_preprocessor (callable, optional) – A callable potentially applying transformations or checks to the phenome.
kwargs – Arbitrary keyword arguments, passed through to the constructor of the super class.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.himmelblau(phenome)¶: The bare-bones Himmelblau function.

class optproblems.continuous.Himmelblau(phenome_preprocessor=None, **kwargs)¶

Himmelblau’s test problem.

No bound constraints are pre-defined for this problem. Possible choices including all the optima are $[-4, 4] \times [-4, 4]$ or larger rectangles.

References

[Himmelblau1972]

David M. Himmelblau, Applied Nonlinear Programming, McGraw Hill, 1972

get_locally_optimal_solutions(max_number=None)¶

Return the four optimal solutions.

All local optima are global optima in this problem.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶

Return the four optimal solutions.

All local optima are global optima in this problem.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

optproblems.continuous.griewank(phenome)¶: The bare-bones Griewank function.

class optproblems.continuous.Griewank(num_variables=10, phenome_preprocessor=None, **kwargs)¶

Griewank’s test problem.

No bound constraints are pre-defined for this problem. A possible choice is $[-600, 600]$ for each variable.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.LunacekTwoSpheres(num_variables=10, depth=0.0, size=1.0, phenome_preprocessor=None, **kwargs)¶

Lunacek’s two spheres.

References

[Lunacek2008]

M. Lunacek, D. Whitley, and A. Sutton (2008). The Impact of Global Structure on Search. In: Parallel Problem Solving from Nature, Lecture Notes in Computer Science, vol. 5199, pp. 498-507, Springer.

__init__(num_variables=10, depth=0.0, size=1.0, phenome_preprocessor=None, **kwargs)¶

Constructor.

Parameters:	num_variables (int, optional) – Number of decision variables of the problem. depth (float, optional) – Depth parameter of the worse basin. size (float, optional) – Size parameter of the worse basin. kwargs – Arbitrary keyword arguments, passed through to the constructor of the super class.

get_locally_optimal_solutions(max_number=None)¶

Return the locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.LunacekTwoRastrigins(num_variables=10, depth=0.0, size=1.0, a=10.0, omega=6.283185307179586, **kwargs)¶

Lunacek’s two Rastrigin functions.

__init__(num_variables=10, depth=0.0, size=1.0, a=10.0, omega=6.283185307179586, **kwargs)¶

Constructor.

Parameters:

num_variables (int, optional) – Number of decision variables of the problem.
depth (float, optional) – Depth parameter of the worse basin.
size (float, optional) – Size parameter of the worse basin.
a (float, optional) – Amplitude of the cosine term of the rastrigin function.
omega (float, optional) – Controls the period length of the cosine term of the rastrigin function.
kwargs – Arbitrary keyword arguments, passed through to the constructor of the super class.

class optproblems.continuous.ModifiedRastriginFunction(num_variables, omegas, k_values)¶

A function similar to the Rastrigin function.

The basic one-dimensional formula reads 2.0 * k * x ** 2 + 10.0 * cos(omega * x). Further information can be found in [Saha2010].

__call__(phenome)¶: Evaluate the function.

class optproblems.continuous.ModifiedRastrigin(num_variables=16, k_values=None, phenome_preprocessor=None, **kwargs)¶

A test problem similar to the Rastrigin problem.

The modification consists of a configurable number of local optima per dimension, so that the total number of local optima becomes less dependent on the dimension. The problem was defined in [Saha2010]. There are three pre-defined instances with 4, 8, and 16 variables, respectively, which can be obtained from the create_instance method. The search space is the unit hypercube.

References

[Saha2010]

(1, 2) Amit Saha, Kalyanmoy Deb (2010). A Bi-criterion Approach to Multimodal Optimization: Self-adaptive Approach. In: Simulated Evolution and Learning, vol. 6457 of Lecture Notes in Computer Science, pp. 95-104, Springer

static create_instance(num_variables, **kwargs)¶

Factory method for pre-defined modified Rastrigin problems.

Parameters:	num_variables (int) – Must be 4, 8, or 16. kwargs – Arbitrary keyword arguments, passed through to the constructor.
Returns:	problem
Return type:	ModifiedRastrigin instance

get_locally_optimal_solutions(max_number=None)¶

Return locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

class optproblems.continuous.RastriginFunction(a=10.0, omega=6.283185307179586)¶

A configurable Rastrigin function.

The basic one-dimensional formula reads x ** 2 - a * cos(omega * x).

__call__(phenome)¶: Evaluate the function.

class optproblems.continuous.Rastrigin(num_variables=10, a=10.0, omega=6.283185307179586, phenome_preprocessor=None, **kwargs)¶

A configurable Rastrigin test problem.

No bound constraints are pre-defined for this problem, but $[-5, 5]$ for every variable is a typical choice.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.rosenbrock(phenome)¶: The bare-bones Rosenbrock function.

class optproblems.continuous.Rosenbrock(num_variables=10, phenome_preprocessor=None, **kwargs)¶

Rosenbrock’s test problem.

No bound constraints are pre-defined for this problem.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.schaffer6(phenome)¶: The bare-bones Schaffer function 6.

class optproblems.continuous.Schaffer6(phenome_preprocessor=None, **kwargs)¶

Schaffer’s test problem 6.

This problem is radially symmetric. Thus it does not possess a discrete set of local optima. It was defined for two dimensions in [Schaffer1989]. The global optimum is the origin and the search space is $[-100, 100] \times [-100, 100]$ .

References

[Schaffer1989]

(1, 2) Schaffer, J. David; Caruana, Richard A.; Eshelman, Larry J.; Das, Rajarshi (1989). A study of control parameters affecting online performance of genetic algorithms for function optimization. In: Proceedings of the third international conference on genetic algorithms, pp. 51-60, Morgan Kaufmann.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.schaffer7(phenome)¶: The bare-bones Schaffer function 7.

class optproblems.continuous.Schaffer7(phenome_preprocessor=None, **kwargs)¶

Schaffer’s test problem 7.

This problem is radially symmetric. Thus it does not possess a discrete set of local optima. It was defined for two dimensions in [Schaffer1989]. The global optimum is the origin and the search space is $[-100, 100] \times [-100, 100]$ .

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.schwefel(phenome)¶: The bare-bones Schwefel function.

class optproblems.continuous.Schwefel(num_variables=10, phenome_preprocessor=None, **kwargs)¶

Schwefel’s test problem.

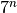Note that bound constraints are required for the global optimum to exist. $[-500, 500]$ for each variable is the default here. Then the problem has $7^n$ local optima.

get_locally_optimal_solutions(max_number=None)¶

Return the locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.six_hump_camelback(phenome)¶: The bare-bones six-hump camelback function.

class optproblems.continuous.SixHumpCamelback(phenome_preprocessor=None, **kwargs)¶

The so-called six-hump camelback test problem.

No bound constraints are pre-defined for this problem. Possible choices including all the optima are $[-1.9, 1.9] \times [-1.1, 1.1]$ or larger rectangles.

get_locally_optimal_solutions(max_number=None)¶

Return the locally optimal solutions.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶: Return the two global optima.

optproblems.continuous.sphere(phenome)¶: The bare-bones sphere function.

class optproblems.continuous.Sphere(num_variables=10, phenome_preprocessor=None, **kwargs)¶

The sphere problem.

Possibly the most simple unimodal problem. No bound constraints are pre-defined.

get_locally_optimal_solutions(max_number=None)¶: Return the global optimum.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

optproblems.continuous.vincent(phenome)¶: The bare-bones Vincent function.

class optproblems.continuous.Vincent(num_variables=5, phenome_preprocessor=None, **kwargs)¶

Vincent’s test problem.

All variables have lower and upper bounds of 0.25 and 10, respectively. The problem has 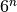$6^n$ global optima.

get_locally_optimal_solutions(max_number=None)¶

Return the optimal solutions.

All local optima are global optima in this problem.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

get_optimal_solutions(max_number=None)¶

Return the optimal solutions.

All local optima are global optima in this problem.

Parameters:	max_number (int, optional) – Potentially restrict the number of optima.
Returns:	optima
Return type:	list of Individual

class optproblems.continuous.WeierstrassFunction(a=0.5, b=3.0, k_max=20)¶

A configurable Weierstrass function.

__call__(phenome)¶: Evaluate the function.

class optproblems.continuous.Weierstrass(num_variables=10, a=0.5, b=3.0, k_max=20, phenome_preprocessor=None, **kwargs)¶

Weierstrass’ test problem.

No bound constraints are pre-defined for this problem.

get_optimal_solutions(max_number=None)¶: Return the global optimum.

Examples¶

Modifying existing bounds:

from optproblems.continuous import Branin
branin = Branin()
# raises BoundConstraintError
branin([16.0, 16.0])
# alter bounds
branin.max_bounds = [20.0, 20.0]
# now admissible
branin([16.0, 16.0])

However, if no bound constraints were previously defined, you also have to add a BoundConstraintsChecker preprocessor for bounds to be checked.

from optproblems import *
from optproblems.continuous import Sphere
sphere = Sphere(2)
sphere.min_bounds = [-5.0, -5.0]
sphere.max_bounds = [5.0, 5.0]
# still not checked
sphere([10.0, 10.0])
bounds = ([-5.0, -5.0], [5.0, 5.0])
preprocessor = BoundConstraintsChecker(bounds)
sphere = Sphere(2, phenome_preprocessor=preprocessor)
# now the exception is raised
sphere([10.0, 10.0])
# however, bounds are not automatically saved as problem attributes
sphere.min_bounds  # raises AttributeError

Note

If you modify constraints, the information obtained from get_optimal_solutions and get_locally_optimal_solutions may be incorrect, i.e., returned solutions may be actually infeasible.

`continuous` — Real-valued Test Problems¶

Dixon-Szegö Collection¶

Other Problems¶

Examples¶

Table Of Contents

Previous topic

Next topic

This Page

continuous — Real-valued Test Problems¶

Dixon-Szegö Collection¶

Other Problems¶

Examples¶

`continuous` — Real-valued Test Problems¶