`algo` — Evolutionary Algorithms¶

This module contains evolutionary algorithms and some related classes.

EvolutionaryAlgorithm is the base class for all other algorithms.

class evoalgos.algo.EvolutionaryAlgorithm(problem, start_population, population_size, num_offspring, max_age, reproduction, selection, max_generations=inf, archive=None, verbosity=1, lock=None, **kwargs)¶

A modular evolutionary algorithm.

Apart from the arguments provided in the constructor, this class possesses the potentially useful member attributes remaining_generations, generation, and last_termination. The latter attribute stores the exception instance that caused the last termination.

__init__(problem, start_population, population_size, num_offspring, max_age, reproduction, selection, max_generations=inf, archive=None, verbosity=1, lock=None, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – An optimization problem.
start_population (list of Individual) – A list of individuals.
population_size (int) – The number of individuals that will survive the selection step in each generation.
num_offspring (int) – The number of individuals born in every generation.
max_age (int) – A maximum number of generations an individual can live. This number may be exceeded if not enough offspring is generated to reach the population_size.
reproduction (Reproduction) – A Reproduction object selecting the parents for mating and creating the offspring.
selection (Selection) – A Selection object carrying out the survivor selection.
max_generations (int, optional) – A potential budget restriction on the number of generations. Default is unlimited.
archive (list of Individual, optional) – Individuals that may influence the survivor selection. This data structure is by default not modified by the evolutionary algorithm.
verbosity (int, optional) – A value of 0 means quiet, 1 means some information is printed to standard out on start and termination of this algorithm.
lock (threading.Lock, optional) – A mutex protecting all read and write accesses to the population. This is necessary for asynchronous parallelization of the EA. See the parallelization example.

__str__()¶: Return the algorithm’s name.

run()¶

Run the algorithm.

After an initial evaluation of individuals with invalid objective values, the step() function is called in a loop. The algorithm stops when a StopIteration exception is caught or when the stopping criterion evaluates to True.

step()¶: Carry out a single step of optimization.

stopping_criterion()¶

Check if optimization should go on.

The algorithm halts when this method returns True or raises an exception.

Raises:	`ResourcesExhausted` – When the number of generations reaches the maximum.

survivor_selection(parents, offspring, num_survivors)¶

Carry out survivor selection.

Parents and offspring are treated differently in this method. A parent may be removed because it is too old or because it has a bad fitness. Offspring individuals can only be removed because of bad fitness. The fitness is determined by the EA’s selection component. (Note that fitness is not necessarily equivalent to an individual’s objective values.)

This method guarantees that exactly num_survivors individuals survive, as long as len(parents) + len(offspring) >= num_survivors. To ensure this invariant, the best of the too old parents may be retained in the population, although their maximum age is technically exceeded. If len(parents) + len(offspring) < num_survivors, no one is removed.

Parameters:

parents (list of Individual) – Individuals in the parent population.
offspring (list of Individual) – Individuals in the offspring population.
num_survivors (int) – The number of surviving individuals.

Returns:

population (list) – The survivors of the selection.
rejected (list) – Individuals removed due to bad fitness.
deceased (list) – Rejected + individuals who died of old age.

class evoalgos.algo.CommaEA(problem, start_population, population_size, num_offspring, reproduction=None, selection=None, **kwargs)¶

An evolutionary algorithm with so-called comma selection.

In this EA, individuals live at most one generation. This is assumed to be somewhat beneficial on multimodal and dynamic problems. Typically, this algorithm is used in combination with the self-adaptive step-size control provided by ESIndividual or CMSAIndividual. For more information, see [Beyer2002].

__init__(problem, start_population, population_size, num_offspring, reproduction=None, selection=None, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – An optimization problem.
start_population (list of Individual) – A list of individuals.
population_size (int) – The number of individuals that will survive the selection step in each generation.
num_offspring (int) – The number of individuals born in every generation.
reproduction (Reproduction, optional) – A Reproduction object selecting the parents for mating and creating the offspring. By default, ESReproduction is chosen.
selection (Selection, optional) – A Selection object carrying out the survivor selection. By default, TruncationSelection based on LexicographicSorting is used.
kwargs – Arbitrary keyword arguments, passed to the super class.

class evoalgos.algo.PlusEA(problem, start_population, population_size, num_offspring, reproduction=None, selection=None, **kwargs)¶

An evolutionary algorithm with so-called plus selection.

In this EA, no maximum age is set for individuals. This is especially suitable for unimodal problems. Typically, this algorithm is used in combination with the self-adaptive step-size control provided by ESIndividual. For more information, see [Beyer2002].

__init__(problem, start_population, population_size, num_offspring, reproduction=None, selection=None, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – An optimization problem.
start_population (list of Individual) – A list of individuals.
population_size (int) – The number of individuals that will survive the selection step in each generation.
num_offspring (int) – The number of individuals born in every generation.
reproduction (Reproduction, optional) – A Reproduction object selecting the parents for mating and creating the offspring. By default, ESReproduction is chosen.
selection (Selection, optional) – A Selection object carrying out the survivor selection. By default, TruncationSelection based on LexicographicSorting is used.
kwargs – Arbitrary keyword arguments, passed to the super class.

class evoalgos.algo.CMSAES(problem, start_population, population_size=None, num_offspring=None, max_age=1, reproduction=None, selection=None, xtol=None, steptol=None, **kwargs)¶

Covariance matrix self-adaptation ES.

This is a convenience class for easy setup of this algorithm. For more information on the working principle of the algorithm, see [Beyer2008].

__init__(problem, start_population, population_size=None, num_offspring=None, max_age=1, reproduction=None, selection=None, xtol=None, steptol=None, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – An optimization problem.
start_population (list of Individual) – A list of individuals.
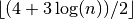population_size (int, optional) – The number of individuals that will survive the selection step in each generation. The default is $\lfloor(4 + 3 \log(n))/2\rfloor$ .
num_offspring (int, optional) – The number of individuals born in every generation. Default is four times the population size.
max_age (int, optional) – A maximum number of generations an individual can live. This number may be exceeded if not enough offspring is generated to reach the population_size.
reproduction (Reproduction, optional) – A Reproduction object selecting the parents for mating and creating the offspring. By default, ESReproduction is chosen.
selection (Selection, optional) – A Selection object carrying out the survivor selection. By default, TruncationSelection based on LexicographicSorting is used.
xtol (float, optional) – The algorithm stops when the maximal absolute deviation in all dimensions of the search space between the best and all other solutions in the population drops below this value. By default, this criterion is off.
steptol (float, optional) – The algorithm stops when the mutation strength parameters of all the individuals in the population drop below this value.
kwargs – Arbitrary keyword arguments, passed to the super class.

classmethod minimize(fun, x0, args=(), bounds=None, callback=None, options=None, **kwargs)¶

Minimization of scalar function of one or more variables.

This function mimics the SciPy interface for optimizers.

Parameters:	fun (callable) – Objective function. x0 (sequence) – Initial guess. args (tuple, optional) – Extra arguments passed to the objective function. bounds (sequence, optional) – Bounds for variables. `(min, max)` pairs for each element in `x`, defining the bounds on that parameter. Use None for one of `min` or `max` when there is no bound in that direction. callback (callable, optional) – Called after each iteration, as `callback(xk)`, where `xk` is the current parameter vector. options (dict, optional) – A dictionary of solver options. The following generic options are accepted: maxiter : int Maximum number of iterations to perform. disp : bool Set to True to print convergence messages.
Returns:	result – The optimization result represented as a `OptimizeResult` object. Important attributes are: `x` the solution array, `success` a Boolean flag indicating if the optimizer exited successfully and `message` which describes the cause of the termination.
Return type:	OptimizeResult

stopping_criterion()¶

Check if optimization should go on.

The algorithm halts when this method returns True or raises an exception.

Raises:	`ResourcesExhausted` – When the number of generations reaches the maximum. `Stalled` – When a dispersion-related key figure of the population drops below a threshold.

class evoalgos.algo.NSGA2b(problem, start_population, population_size, num_offspring=None, reproduction=None, do_backward_elimination=True, **kwargs)¶

An enhanced non-dominated sorting genetic algorithm 2.

The algorithm was originally devised by [Deb2000]. In this implementation, the improved selection proposed by [Kukkonen2006] is used by default (although not with any special data structures as in the paper). Also the number of offspring can be chosen freely in contrast to the original definition, so that also a (mu + 1)-approach as in [Durillo2009] is possible.

Warning

This algorithm should only be used for two objectives, as the selection criterion is not suited for higher dimensions.

References

[Deb2000]

Kalyanmoy Deb, Samir Agrawal, Amrit Pratap, and T Meyarivan (2000). A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In: Parallel Problem Solving from Nature, PPSN VI, Volume 1917 of Lecture Notes in Computer Science, pp 849-858, Springer. https://dx.doi.org/10.1007/3-540-45356-3_83

[Kukkonen2006]

Kukkonen, Saku; Deb, Kalyanmoy (2006).Improved Pruning of Non-Dominated Solutions Based on Crowding Distance for Bi-Objective Optimization Problems. In: IEEE Congress on Evolutionary Computation, pp. 1179-1186. https://dx.doi.org/10.1109/CEC.2006.1688443

[Durillo2009]

Juan J. Durillo, Antonio J. Nebro, Francisco Luna, Enrique Alba (2009). On the Effect of the Steady-State Selection Scheme in Multi-Objective Genetic Algorithms. In: Evolutionary Multi-Criterion Optimization, Volume 5467 of Lecture Notes in Computer Science, pp 183-197, Springer. https://dx.doi.org/10.1007/978-3-642-01020-0_18

__init__(problem, start_population, population_size, num_offspring=None, reproduction=None, do_backward_elimination=True, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – A multiobjective optimization problem.
start_population (list of Individual) – The initial population of individuals. The size of this list does not have to be the same as population_size, but will be adjusted subsequently.
population_size (int) – The number of individuals that will survive the selection step in each generation.
num_offspring (int, optional) – The number of individuals born in every generation. By default, this value is set equal to the population size.
reproduction (Reproduction, optional) – A Reproduction object selecting the parents for mating and creating the offspring. If no object is provided, a default variant is generated, which selects parents uniformly random.
do_backward_elimination (bool, optional) – This argument only has influence if num_offspring > 1. Backward elimination means that in a greedy fashion, the worst individuals are removed one by one. The alternative is the original ‘super-greedy’ approach, which removes the necessary number of individuals without recalculating the fitness of the other ones in between. Default is True (the former approach), which is also recommended, because it is more accurate.
kwargs – Further keyword arguments passed to the constructor of the super class.

class evoalgos.algo.SMSEMOA(problem, start_population, population_size, num_offspring=1, reproduction=None, prefer_boundary_points=True, selection_variant='auto', offsets=None, **kwargs)¶

The S-metric Selection EMOA.

This multiobjective optimization algorithm uses a solution’s exclusive contribution to the hypervolume of the worst non-dominated front of a population as a selection criterion. (Hypervolume was formerly known as S-metric.) The algorithm was proposed in [Emmerich2005] and [Naujoks2005].

Warning

The time for calculating the hypervolume is exponential in the number of objectives.

References

[Emmerich2005]

Michael Emmerich, Nicola Beume, Boris Naujoks (2005). An EMO Algorithm Using the Hypervolume Measure as Selection Criterion. In: Evolutionary Multi-Criterion Optimization, Volume 3410 of Lecture Notes in Computer Science, pp 62-76, Springer. https://dx.doi.org/10.1007/978-3-540-31880-4_5

[Naujoks2005]

Boris Naujoks, Nicola Beume, Michael Emmerich (2005). Multi-objective optimisation using S-metric selection: application to three-dimensional solution spaces. In: The 2005 IEEE Congress on Evolutionary Computation, vol.2, pp.1282-1289, IEEE Press. https://dx.doi.org/10.1109/CEC.2005.1554838

__init__(problem, start_population, population_size, num_offspring=1, reproduction=None, prefer_boundary_points=True, selection_variant='auto', offsets=None, **kwargs)¶

Constructor.

Parameters:

problem (optproblems.Problem) – A multiobjective optimization problem.
start_population (list of Individual) – The initial population of individuals. The size of this list does not have to be the same as population_size, but will be adjusted subsequently.
population_size (int) – The number of individuals that will survive the selection step in each generation.
num_offspring (int, optional) – The number of individuals born in every generation. This value is typically 1, but the implementation also admits larger values.
reproduction (Reproduction, optional) – A Reproduction object selecting the parents for mating and creating the offspring. If no object is provided, a default variant is generated, which selects parents uniformly random.
prefer_boundary_points (bool, optional) – This flag only pertains to the two-objective case. If it is set to True, the two boundary points (but not their potentially existing duplicates) of a front are guaranteed to be retained.
selection_variant (string, optional) – This argument has the possible values ‘forward-greedy’, ‘backward-greedy’, ‘super-greedy’, and ‘auto’. ‘backward-greedy’ means that the worst individuals are iteratively removed one by one (also known as backward elimination). ‘forward-greedy’ means that also iteratively, the individual maximizing the hypervolume together with the already selected ones is chosen. ‘auto’ selects forward selection if 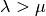$\lambda > \mu$ , and backward elimination otherwise. This rule was devised based on results in [Schendekehl2017]. Finally, ‘super-greedy’ removes the necessary number of individuals without recalculating the fitness of the other ones in between (this is faster, but not recommended). We have to know the variant internally, because the results of the wrapper approach with BackwardElimination or ForwardSelection are not 100% correct (due to reference point construction being triggered in every iteration) and because some time can be saved.
offsets (list, optional) – For calculating the hypervolume, a reference point is required. The reference point is typically calculated as the worst objective values in the last front plus an offset vector, which can be specified here. Default offset is [1.0, ..., 1.0].
kwargs – Further keyword arguments passed to the constructor of the super class.

Examples¶

In this section we show how to set up some of the provided algorithms.

CMSA-ES¶

The CommaEA together with the CMSAIndividual yields the covariance matrix self-adaptation evolution strategy (CMSA-ES). Note that CMSA-ES is not to be confused with CMA-ES.

import array
import random
from optproblems.continuous import DoubleSum
from evoalgos.algo import CommaEA
from evoalgos.individual import CMSAIndividual

dim = 10
problem = DoubleSum(dim, max_evaluations=5000)
popsize = 5
num_offspring = 4 * popsize
population = []
for _ in range(popsize):
    ind = CMSAIndividual(num_parents=popsize, num_offspring=num_offspring)
    ind.genome = [random.uniform(-20.0, 20.0) for _ in range(dim)]
    # for lowest CPU time, array.array is recommended
    ind.genome = array.array("d", ind.genome)
    population.append(ind)

ea = CommaEA(problem, population, popsize, num_offspring)
ea.run()
print(ea.population[0].objective_values, problem.consumed_evaluations)

However, there is also a convenience class CMSAES that sets several arguments with default values. The easiest way to use it is via the minimize() classmethod that mimics the interface of SciPy optimizers.

from evoalgos.algo import CMSAES

def sphere(phenome):
    return sum(x * x for x in phenome)

result = CMSAES.minimize(sphere, [1.333, 1.999])

SMS-EMOA¶

In this example, we create an instance of the SMS-EMOA and let it run on a toy problem.

import math
import random
from optproblems import Problem
from evoalgos.algo import SMSEMOA
from evoalgos.individual import ESIndividual

def obj_function(phenome):
    return sum(x ** 2 for x in phenome), sum((x - 2) ** 2 for x in phenome)

problem = Problem(obj_function, num_objectives=2, max_evaluations=1000, name="Example")
dim = 10
popsize = 10
population = []
init_step_sizes = [0.25]
for _ in range(popsize):
    population.append(ESIndividual(genome=[random.random() * 5 for _ in range(dim)],
                                   learning_param1=1.0/math.sqrt(dim),
                                   learning_param2=0.0,
                                   strategy_params=init_step_sizes,
                                   recombination_type="none",
                                   num_parents=1))

ea = SMSEMOA(problem, population, popsize, num_offspring=40)
ea.run()
for individual in ea.population:
    print(individual)

Parallelization¶

All EAs in this package are prepared for parallel execution. The example below contains both synchronous and asynchronous parallelization of the SMS-EMOA. In this example, a problem with two objectives is optimized with a parallelization degree of four and 1000 evaluations. The code works the same way for the steady-state NSGA2 by simply substituting the appearances of SMSEMOA with NSGA2b. Also the adaptation to the single-objective case should be straightforward.

Note that the asynchronous implementation uses the threading-API, so a real-world objective function must be a wrapper to a blocking system call to obtain truly parallel execution of evaluations. The parallelization in the synchronous case is provided by optproblems.base.Problem, which alternatively supports multiprocessing.

import time
from threading import Lock, Thread
from multiprocessing.dummy import Pool
from random import random

from optproblems import Problem
from evoalgos.algo import SMSEMOA
from evoalgos.individual import SBXIndividual

def obj_function(p):
    time.sleep(0.01)
    return sum(x ** 2 for x in p), sum((x - 2) ** 2 for x in p)

# initialization
parallelism = 4
popsize = 100
population = []
pool = Pool(processes=parallelism)
problem = Problem(obj_function, num_objectives=2, worker_pool=pool)
for _ in range(popsize):
    population.append(SBXIndividual(genome=[random() * 5 for _ in range(8)]))

problem.batch_evaluate(population)
# asynchronous optimization
problem.remaining_evaluations = 1000
lock = Lock()
eas = []
for _ in range(parallelism):
    eas.append(SMSEMOA(problem, population, len(population), 1, lock=lock))

threads = [Thread(target=ea.run) for ea in eas]
for thread in threads:
    thread.start()

for thread in threads:
    thread.join()

# synchronous optimization
problem.remaining_evaluations = 1000
ea = SMSEMOA(problem, population, len(population), parallelism)
ea.run()
pool.close()
pool.join()

`algo` — Evolutionary Algorithms¶

Examples¶

CMSA-ES¶

SMS-EMOA¶

Parallelization¶

Table Of Contents

Previous topic

Next topic

This Page

algo — Evolutionary Algorithms¶

Examples¶

CMSA-ES¶

SMS-EMOA¶

Parallelization¶

`algo` — Evolutionary Algorithms¶