subset — Select diverse subsets

This module contains algorithms for the task of subset selection: suppose you have a set of points in 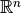\mathbb{R}^n and want to select a sample of them distributed as uniform as possible. This problem is related to clustering, with the difference that when using clustering, you usually want to retain the structure of the original point set.

Part-and-select algorithm

class diversipy.subset.MinBoundingBox(all_points, member_indices)

Data structure containing some information about a cluster of points.

The box does not store the points themselves, but merely a reference to a container of a (possibly) larger set of points and the indices of points in this container belonging to this box. Most importantly, the box holds cached information about the minimal and maximal coordinates of the points and the largest difference between them. This information is important for the part-and-select algorithm (PSA) [Salomon2013]. Comparison operators are overloaded to compare by this value for easy use in a binary heap.

closest_point_index(sought_point, candidate_indices, dist_matrix_function=None)

Return the index of the point closest to a certain target.

Parameters:
  • sought_point (array_like) – The target point.
  • candidate_indices (array_like) – Indices into the container of all points for the candidates to be considered.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

closest_point_index
Return type:

integer
obtain_representative(selection_target='centroid_of_hypercube', tournament_size=0, dist_matrix_function=None)

Return a point representing this cluster.

Parameters:
  • selection_target (string, optional) – Indicates which strategy is used to determine a representative. This must be one of (‘random_uniform’, ‘centroid_of_hypercube’, ‘center_of_mass’, ‘max_dist_from_boundary’).
  • tournament_size (int, optional) – Optionally restrict the candidates for selection to 0 < tournament_size < len(member_indices) randomly chosen points. Any other value of this parameter leads to consideration of all points. Note that a value of 1 leads to a random choice among the clusters members, regardless of the target point.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance. This choice does not affect the selection strategy max_dist_from_boundary.
Returns:

representative
Return type:

array_like
obtain_representative_index(selection_target='centroid_of_hypercube', tournament_size=0, dist_matrix_function=None)

Return the index to a point representing this cluster.

Parameters:
  • selection_target (string, optional) – Indicates which strategy is used to determine a representative. This must be one of (‘random_uniform’, ‘centroid_of_hypercube’, ‘center_of_mass’, ‘max_dist_from_boundary’).
  • tournament_size (int, optional) – Optionally restrict the candidates for selection to 0 < tournament_size < len(member_indices) randomly chosen points. Any other value of this parameter leads to consideration of all points. Note that a value of 1 leads to a random choice among the clusters members, regardless of the target point.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance. This choice does not affect the selection strategy max_dist_from_boundary.
Returns:

representative_index
Return type:

int
update_information()

Gather information from the points and save it.

diversipy.subset.psa_partition(points, num_clusters, available_points_indices=None)

Partition the data set into the given number of clusters.

The approach was originally proposed in [Salomon2013]. The implementation here is the slightly improved version from [Wessing2015].

Note

This algorithm fails if there are less than num_clusters distinct points in the original set.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • num_clusters (int) – The number of ‘clusters’ to be identified.
  • available_points_indices (array_like, optional) – If desired, the set of considered points can already be restricted here by only providing a subset of the indices into points.
Returns:

clusters
Return type:

list of MinBoundingBox

References

[Salomon2013](1, 2, 3) Salomon, Shaul; Avigad, Gideon; Goldvard, Alex; Schütze, Oliver (2013). PSA – A New Scalable Space Partition Based Selection Algorithm for MOEAs. EVOLVE – A Bridge between Probability, Set Oriented Numerics, and Evolutionary Computation II, Advances in Intelligent Systems and Computing, Springer, Vol. 175, pp. 137-151. https://dx.doi.org/10.1007/978-3-642-31519-0_9
diversipy.subset.psa_select(points, num_selected_points, available_points_indices=None, selection_target='centroid_of_hypercube', tournament_size=0, dist_matrix_function=None)

Combine partitioning and determination of representatives.

The approach was originally proposed in [Salomon2013]. The implementation here is the slightly improved version from [Wessing2015].

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • num_selected_points (int) – The number of points to be selected.
  • available_points_indices (array_like, optional) – If desired, the set of considered points can already be restricted here by only providing a subset of the indices into points.
  • selection_target (string, optional) – Indicates which strategy is used to determine a representative. This must be one of (‘random_uniform’, ‘centroid_of_hypercube’, ‘center_of_mass’, ‘max_dist_from_boundary’).
  • tournament_size (int, optional) – Optionally restrict the candidates for selection to 0 < tournament_size < len(member_indices) randomly chosen points. Any other value of this parameter leads to consideration of all points. Note that a value of 1 leads to a random choice among the clusters members, regardless of the target point.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance. This choice does not affect the selection strategy max_dist_from_boundary.
Returns:

representatives
Return type:

array_like

Greedy algorithms

The algorithms in this group all follow the same pattern: they start with an empty set and add one point per iteration. The selected point is the one with the best assessment with regard to the already selected points, hence the classification as greedy methods. The first point is chosen with regard to the existing points. If no existing points are given, one of the candidate points is randomly selected to act as an existing point. So, to enforce a deterministic behavior, provide at least one existing point. The run time is 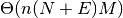\Theta(n(N+E)M) for n dimensions, M candidates, E existing, and N selected points.

diversipy.subset.select_greedy_maximin(points, num_selected_points, existing_points=None, dist_matrix_function=None)

Greedily select a subset according to maximin criterion.

This selection approach corresponds to the indicator separation_dist().

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • num_selected_points (int) – The number of points to be selected.
  • existing_points (array_like, optional) – Points that cannot be modified anymore, but should be considered in the distance computations.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

selected_points
Return type:

array_like
diversipy.subset.select_greedy_maxisum(points, num_selected_points, existing_points=None, dist_matrix_function=None)

Greedily select a subset according to maxisum criterion.

This selection approach corresponds to the indicator sum_of_dists().

Warning

This function does not result in a uniformly distributed subset of the points, instead it selects extremal points.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • num_selected_points (int) – The number of points to be selected.
  • existing_points (array_like, optional) – Points that cannot be modified anymore, but should be considered in the distance computations.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

selected_points
Return type:

array_like
diversipy.subset.select_greedy_energy(points, num_selected_points, existing_points=None, exponent=None, dist_matrix_function=None)

Greedily select a subset according to potential energy.

This selection approach uses the Riesz energy as selection criterion, which is related to the indicator average_inverse_dist(). The uniformity of the selected points can be controlled by exponent. More information about this criterion can for example be found in [Hardin2004].

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • num_selected_points (int) – The number of points to be selected.
  • existing_points (array_like, optional) – Points that cannot be modified anymore, but should be considered in the distance computations.
  • exponent (int or float, optional) – Parameter controlling the uniformity. Must be >= 0. Values greater or equal the dimension lead to uniformity, smaller values to a higher density in exterior regions.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

selected_points
Return type:

array_like

References

[Hardin2004]Hardin, Douglas P.; Saff, Ed B. (2004). Discretizing Manifolds via Minimum Energy Points. Notices of the American Mathematical Society, Vol. 51, No. 10, pp. 1186-1194. http://www.math.vanderbilt.edu/~hardin/papers/HSb2004.pdf