indicator — Useful diversity indicators

This module contains several functions to measure diversity and a few related concepts. The diversity indicators all have different advantages and disadvantages. An overview is given in [Wessing2015].

Diversity indicators

diversipy.indicator.covering_radius(points, repair_margin=1e-08, full_output=False)

Calculate the covering radius of points in the unit hypercube.

The indicator is calculated for Euclidean distance via a Voronoi tessellation. It should be minimized. Coordinates of points must be >0 and <1.

Note

This function requires SciPy for the Voronoi tessellation.

Warning

The run time is exponential in the dimension.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • repair_margin (float, optional) – Due to the inherent inaccuracy of floating point arithmetic, some vertices of the Voronoi tessellation that should be exactly on a boundary may be located outside the hypercube. This parameter specifies a margin around the hypercube, whose points are repaired and included in the distance calculations. The higher this value, the more expensive and the more reliable are the calculations.
  • full_output (bool, optional) – If true, also the Voronoi tessellation itself is returned.
Returns:

  • cov_radius (float) – The covering radius of the point set.
  • voronoi_tessellation (scipy.spatial.qhull.Voronoi) – Data structure containing the Voronoi tessellation produced by the Qhull library. See SciPy documentation for details.
diversipy.indicator.covering_radius_ub(points, strata, dist_matrix_function=None)

Upper bound for the covering radius.

Parameters:
  • points (array_like) – The points to assess.
  • strata (sequence of tuple) – A partition of the unit hypercube as produced by stratified_sampling with full_output enabled. Each stratum must contain exactly one point.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

cr_ub – Upper bound of the covering radius for the point set.
Return type:

float
diversipy.indicator.covering_radius_lb(points, num_monte_carlo_points, block_size=10000, dist_matrix_function=None)

Monte Carlo lower bound for the covering radius.

Parameters:
  • points (array_like) – The points to assess.
  • num_monte_carlo_points (int) – The number of points used in the estimation of the covering radius. Higher values lead to a better approximation quality. Points are drawn by stratified sampling in blocks of block_size.
  • block_size (int, optional) – The Monte Carlo points are drawn in blocks of this size to avoid exceeding the memory capacity.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

cr_lb – Lower bound of the covering radius for the point set.
Return type:

float
diversipy.indicator.solow_polasky_diversity(points, activity_param=1.0, dist_matrix_function=None)

Calculate the Solow-Polasky diversity for a set of points.

This diversity indicator was introduced in [Solow1994] and is to be maximized. The algorithm has cubic run time, because the pseudoinverse of a correlation matrix has to be computed. The assumed correlation function is exp(-activity_param * dist).

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • activity_param (float, optional) – Parameter controlling the strength of correlation. It must hold 0 < activity_param <= 2. Default is 1.
  • dist_matrix_function (callable, optional) – A metric distance function. Default is Euclidean distance.
Returns:

diversity
Return type:

float

References

[Solow1994](1, 2) Solow, Andrew R.; Polasky, Stephen (1994). Measuring biological diversity. Environmental and Ecological Statistics, Vol. 1, No. 2, pp. 95-103. https://dx.doi.org/10.1007/BF02426650
diversipy.indicator.weitzman_diversity(points, dist_matrix_function=None)

Calculate the Weitzman diversity for a set of points.

This diversity indicator was introduced in [Weitzman1992]. It is to be maximized.

Warning

This implementation has exponential run time in the number of points!

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

diversity
Return type:

float

References

[Weitzman1992]Weitzman, Martin L. (May 1992). On Diversity. The Quarterly Journal of Economics, Vol. 107, No. 2, pp. 363-405 https://www.jstor.org/stable/2118476
diversipy.indicator.sum_of_dists(points, dist_matrix_function=None)

Calculate the square root of the sum of all pairwise distances.

This indicator is to be maximized.

Warning

This function is only included here for comparisons. It is actually not well suited as diversity indicator, as explained in [Solow1994].

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

spread
Return type:

float
diversipy.indicator.average_inverse_dist(points, exponent=None, max_dist=1.0, dist_matrix_function=None)

Calculate the average inverse distance.

For each pair of points, the value (max_dist / dist) ** exponent is computed. The average of all these values is the indicator value, which is to be minimized.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • exponent (int or float, optional) – Exponent in the calculations explained above. Default is dimension + 1.
  • max_dist (float, optional) – Maximally possible distance or an arbitrary constant.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

diversity
Return type:

float
diversipy.indicator.separation_dist(points, dist_matrix_function=None)

Calculate the minimal pairwise distance.

This indicator is to be maximized.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

min_dist
Return type:

float
diversipy.indicator.wmh_index(sep_dist, dist_p, num_points, dim, approx=None, full_output=False)

Quality index of Wahl, Mercadier, and Helbert.

In [Wahl2017], the idea to use the probability to obtain a sample with a separation distance less or equal to sep_dist was presented. As the exact value is unknown, it has to be approximated. Let the probability be 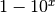1 - 10^{x}, then this function computes 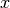x. This value should be minimized. The worst possible value is zero. The decimal library is used internally to obtain a higher precision than conventional floating point arithmetic.

Parameters:
  • sep_dist (float) – The measured separation distance.
  • dist_p (int) – The p of the used 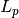L_p distance.
  • num_points (int) – The number of points in the sample.
  • dim (int) – The dimension of the sampled space.
  • approx (sequence, optional) – A sequence of approximation methods to use. Default is (“polynomials”, “gauss”, “gumbel”, “weibull”), which are the four methods presented in [Wahl2017].
  • full_output (bool, optional) – If true, a list of approximation values is returned. Else, the maximum of the used approximations (the most conservative estimate) is returned.
Returns:

approximations – The maximum of the calculated approximations or the whole list of them (according to the order in approx), depending on the switch full_output.
Return type:

float or list

References

[Wahl2017](1, 2) François Wahl, Cécile Mercadier, Céline Helbert (2017). A standardized distance-based index to assess the quality of space-filling designs. Statistics and Computing, Volume 27, Issue 2, pp 319–329. https://dx.doi.org/10.1007/s11222-015-9624-z
diversipy.indicator.sum_of_nn_dists(points, dist_matrix_function=None)

Calculate the sum of nearest-neighbor distances

This indicator is to be maximized.

Parameters:
  • points (array_like) – 2-D data structure holding the points.
  • dist_matrix_function (callable, optional) – An arbitrary distance function. Default is Euclidean distance.
Returns:

sum_of_nn_dists
Return type:

float
diversipy.indicator.unanchored_L2_discrepancy(points)

Calculate unanchored L2 discrepancy.

Discrepancy is to be minimized. Note that the square root is already taken. Coordinates of points must be >=0 and <=1. Run time is quadratic. For details see [Morokoff1994].

Parameters:points (array_like) – 2-D data structure holding the points.
Returns:discrepancy
Return type:float

References

[Morokoff1994](1, 2) Morokoff, William J.; Caflisch, Russel E. (1994). Quasi-random sequences and their discrepancies. SIAM Journal on Scientific Computing, Vol. 15, No. 6, pp. 1251-1279. https://dx.doi.org/10.1137/0915077
diversipy.indicator.expected_unanchored_L2_discrepancy(num_points, dimension)

Expected value for unanchored L2 discrepancy of random uniform points.

Note that this is the square root of 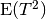\mathrm{E}(T^2), i.e. sqrt(1.0 / n * (6 ** -d) * (1 - 2 ** -d)). For details see [Morokoff1994].