cec2005 — CEC 2005 Problems

This set of 25 test problems was compiled for the Special Session on Real-Parameter Optimization at the Congress on Evolutionary Computation (CEC), Edinburgh, UK, 2-5 Sept. 2005. The mathematical definitions are given in [Suganthan2005]. Additionally, implementations in C, Java, and Matlab were provided for the participants. This code is a reimplementation of the Java code in pure Python.

The correctness of this implementation was verified with the test data distributed with the original code. In accordance with the special session’s guidelines, it is guaranteed for this data that 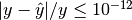|y - \hat{y}|/y \leq 10^{-12} for reference objective values 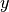y and values 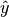\hat{y} calculated here.

Problems F3, F7, F8, F10, F11, F14, and F16-F25 are only defined for 2, 10, 30, and 50 dimensions. The other problems accept an arbitrary number of variables between 1 and 100 (inclusive).

References

[Suganthan2005](1, 2) P. N. Suganthan, N. Hansen, J. J. Liang, K. Deb, Y.-P. Chen, A. Auger, and S. Tiwari. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization. Technical Report, Nanyang Technological University, Singapore, May 2005 and KanGAL Report #2005005, IIT Kanpur, India. http://web.mysites.ntu.edu.sg/epnsugan/PublicSite/Shared%20Documents/CEC2005/Tech-Report-May-30-05.pdf
class optproblems.cec2005.CEC2005(num_variables, **kwargs)

The CEC 2005 problem collection.

The collection was defined in [Suganthan2005]. This class inherits from list and fills itself with 25 problems.

__init__(num_variables, **kwargs)

Constructor.

Parameters:
  • num_variables (int) – The number of decision variables for the problems. Only 2, 10, 30, and 50 are admissible for all problems.
  • kwargs – Arbitrary keyword arguments, passed through to the constructors of the single problems.

Test Problems

The following table gives an overview of the available problems. If bound constraints exist, they are the same for all dimensions. The last column specifies for which dimensions the problems are defined.

Unimodal problems Bounds Deterministic Number variables
optproblems.cec2005.F1 [-100, 100] yes {1, ..., 100}
optproblems.cec2005.F2 [-100, 100] yes {1, ..., 100}
optproblems.cec2005.F3 [-100, 100] yes {2, 10, 30, 50}
optproblems.cec2005.F4 [-100, 100] no {1, ..., 100}
optproblems.cec2005.F5 [-100, 100] yes {1, ..., 100}
Multimodal problems Bounds Deterministic Number variables
optproblems.cec2005.F6 [-100, 100] yes {1, ..., 100}
optproblems.cec2005.F7 none yes {2, 10, 30, 50}
optproblems.cec2005.F8 [-32, 32] yes {2, 10, 30, 50}
optproblems.cec2005.F9 [-5, 5] yes {1, ..., 100}
optproblems.cec2005.F10 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F11 [-0.5, 0.5] yes {2, 10, 30, 50}
optproblems.cec2005.F12 [-pi, pi] yes {1, ..., 100}
optproblems.cec2005.F13 [-3, 1] yes {1, ..., 100}
optproblems.cec2005.F14 [-100, 100] yes {2, 10, 30, 50}
optproblems.cec2005.F15 [-5, 5] yes {1, ..., 100}
optproblems.cec2005.F16 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F17 [-5, 5] no {2, 10, 30, 50}
optproblems.cec2005.F18 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F19 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F20 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F21 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F22 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F23 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F24 [-5, 5] yes {2, 10, 30, 50}
optproblems.cec2005.F25 none yes {2, 10, 30, 50}
class optproblems.cec2005.F1(num_variables, phenome_preprocessor=None, **kwargs)

Shifted sphere.

class optproblems.cec2005.F2(num_variables, phenome_preprocessor=None, **kwargs)

Shifted double-sum.

class optproblems.cec2005.F3(num_variables, phenome_preprocessor=None, **kwargs)

Shifted rotated high conditioned elliptic function.

class optproblems.cec2005.F4(num_variables, phenome_preprocessor=None, **kwargs)

Shifted double-sum with noise.

class optproblems.cec2005.F5(num_variables, phenome_preprocessor=None, **kwargs)

Schwefel’s problem 2.6 with global optimum on bounds.

class optproblems.cec2005.F6(num_variables, phenome_preprocessor=None, **kwargs)

Shifted Rosenbrock’s function.

class optproblems.cec2005.F7(num_variables, **kwargs)

Shifted rotated Griewank’s function without bounds.

class optproblems.cec2005.F8(num_variables, phenome_preprocessor=None, **kwargs)

Shifted rotated Ackley’s function with global optimum on bounds.

class optproblems.cec2005.F9(num_variables, phenome_preprocessor=None, **kwargs)

Shifted Rastrigin’s function.

class optproblems.cec2005.F10(num_variables, phenome_preprocessor=None, **kwargs)

Shifted rotated Rastrigin’s function.

class optproblems.cec2005.F11(num_variables, phenome_preprocessor=None, **kwargs)

Shifted rotated Weierstrass function.

class optproblems.cec2005.F12(num_variables, **kwargs)

Fletcher and Powell’s problem.

class optproblems.cec2005.F13(num_variables, phenome_preprocessor=None, **kwargs)

Expanded extended Griewank’s plus Rosenbrock’s function (F8F2).

class optproblems.cec2005.F14(num_variables, phenome_preprocessor=None, **kwargs)

Shifted rotated expanded Schaffer’s F6.

class optproblems.cec2005.F15(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Hybrid composition function F15.

class optproblems.cec2005.F16(num_variables, matrices=None, offsets=None, **kwargs)

Rotated hybrid composition function F15.

class optproblems.cec2005.F17(num_variables, **kwargs)

Rotated hybrid composition function F16 with noise.

class optproblems.cec2005.F18(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Rotated hybrid composition function F18.

class optproblems.cec2005.F19(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

F18, but with a narrow basin for the global optimum.

class optproblems.cec2005.F20(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Rotated hybrid composition function F18 with global optimum on bounds.

class optproblems.cec2005.F21(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Rotated hybrid composition function F21.

class optproblems.cec2005.F22(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Rotated hybrid composition function F21 with high condition number matrix.

class optproblems.cec2005.F23(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Non-Continuous rotated hybrid composition function F21.

class optproblems.cec2005.F24(num_variables, matrices=None, offsets=None, phenome_preprocessor=None, **kwargs)

Rotated hybrid composition function F24.

class optproblems.cec2005.F25(num_variables, matrices=None, offsets=None, **kwargs)

Rotated hybrid composition function F24 without bounds.