Hypervolume

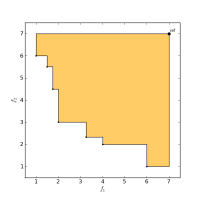
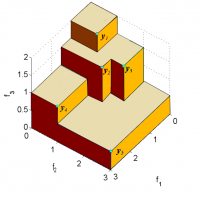
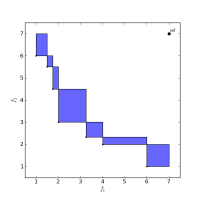
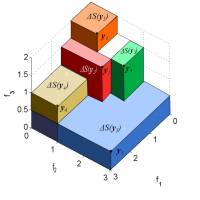
This page presents a collection of links and papers related to the hypervolume quality indicator, a measure often used to assess the performance of multi-objective evolutionary algorithms. It is also used directly inside EAs to provide a selection pressure rewarding convergence as well as objective-space diversity of the candidate solutions. Hypervolume has the drawback that it takes exponential time in the number of dimensions to compute. For this reason, there is an active community developing faster algorithms (in theory and in practice) for this important problem.

(Contributors: Simon Wessing, Boris Naujoks, Michael Emmerich (Leiden U.), Günter Rudolph and Nicola Beume)

• C version by Carlos Fonseca et al. (algorithm description)
• C++ version of HOY by Nicola Beume
• Shark library by Thomas Voß
• Several C++ algorithms in the PaGMO library

• PyGMO library: Python wrapper of PaGMO
• Python version by Simon Wessing is a reimplementation of the code by Fonseca et al. (Variant 3, Version 1.2) in pure Python. Some small modifications have been applied to obtain more performance on the Python interpreter.

# usage example:
from hv import HyperVolume
referencePoint = [2, 2, 2]
hyperVolume = HyperVolume(referencePoint)
front = [[1, 0, 1], [0, 1, 0]]
result = hyperVolume.compute(front)

• R version by Olaf Mersmann

• In The Hypervolume Indicator Revisited: On the Design of Pareto-compliant Indicators Via Weighted Integration (E. Zitzler, D. Brockhoff, and L. Thiele. In S. Obayashi et al., editors, Conference on Evolutionary Multi-Criterion Optimization (EMO 2007), volume 4403 of LNCS, pages 862–876, Berlin, 2007. Springer), the so-called weighted hypervolume indicator has been introduced in order to incorporate specific user preferences into the search.

• The C version implementations of three different bi-objective hypervolume based indicators mentioned in the above paper which incorporate the following preferences: (i) focus on extreme points, (ii) focus on the extremes of the second objective plus one additional extreme point for the first objective, (iii) focus on a given reference point

The S-Metric Selection Evolutionary Multiobjective Optmization Algorithm uses the hypervolume indicator to compute the exclusive hypervolume contribution of solutions.

• As part of the Shark library by Thomas Voß

• MATLAB version by Fabian Kretzschmar and Tobias Wagner (Last Update on March 7, 2016: Implemented Online Convergence Detection according to Wagner, T.; Trautmann, H.: Online Convergence Detection for Evolutionary Multi-Objective Algorithms Revisited. In: Proceedings of the 2010 IEEE Congress on Evolutionary Computation (IEEE CEC 2010), 18.7.-23.7. 2010, Barcelona, Spain, G. Fogel, H. Ishibuchi (Hrsg.), ISBN 978-1-4244-6910-8, S. 3554-3561)

• JMetal version by Simon Wessing

• In the package evoalgos by Simon Wessing

• Gradient of Hypervolume
• Hypervolume contribution
• S-metric-based Expected Improvement (SExI)
• Online Convergence Detection (OCD-Classic and OCD-HV)

• at this time simply as “the size of the space covered”
  • E. Zitzler and L. Thiele. Multiobjective Optimization Using Evolutionary Algorithms - A Comparative Case Study. In Conference on Parallel Problem Solving from Nature (PPSN V), volume 1498 of LNCS, pages 292–301, 1998

• Performance Assessment Indicators comparison: Compatibility and Completeness: Zitzler, Thiele, Laumanns, Fonseca, Grunert da Fonseca (2003)

• Lower Bound Runtime:
  • see Nicola Beume, Carlos M. Fonseca, Manuel López-Ibáñez, Luís Paquete, Jan Vahrenhold, 2009

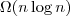
• Worst Case Upper Bound Runtime:
  • see Timothy Chan, 2013

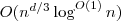
• Complexity of recursive algorithm:
  • see Fonseca et al., 2006

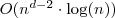
• Fastest implemented algorithm in 4-D Guerreiro, Fonseca, Emmerich 2012

• Approximation
  • fast and precise approximation of 2-dimensional hypervolume, see Tobias Friedrich's homepage

• Runtime Analysis
  • of the 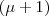-SIBEA on two pseudo-boolean test functions, see D. Brockhoff, T. Friedrich, and F. Neumann. Analyzing Hypervolume Indicator Based Algorithms. In G. Rudolph et al., editors, Conference on Parallel Problem Solving From Nature (PPSN X), volume 5199 of LNCS, pages 651–660. Springer, 2008

• Hypervolume-based Subset Selection and Differential Hypervolume
  • Asymptotically optimal algorithm for computing all differential hypervolume contributions 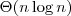in 2-D and 3-D, see Emmerich and Fonseca.
  • Dynamic programming algorithm for 2-D subset selection in 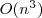, see Auger, Bader, Brockhoff and Zitzler, 2009.
  • 2-D subset selection for hypervolume and epsilon-indicator: Bringmann et al. 2014
  • Upper bounds for complexity of finding the minimal contributor for 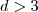: Bringmann and Friedrich.
  • Subset selection NP hardness for n>3, see Rote, Buchin, Bringmann, Cabello, and Emmerich (extended abstract)
  • Set-based Gradient of the hypervolume, see Emmerich, Deutz and Beume and for high dimensions see Emmerich and Deutz

• Optimization Goal of (Weighted, Cone-based) Hypervolume
  • Optimal distribution of 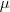points maximizing the (weighted) hypervolume indicator, see Auger, Bader, Brockhoff and Zitzler, 2012.
  • Reference point free weighted hypervolume indicators Emmmerich, Deutz and Yevseyeva.
  • Cone-based hypervolume indicator: efficient computation and 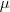-point optimal distributions Emmerich, Deutz, Shukla, and Kruisselbrink 2013

• Expected Hypervolume Improvement in Efficient Global optimization
  • Exact computation and properties Emmerich, Deutz, Klinkenberg 2011
  • Faster Computation Hupkens, Yang, Deutz, Emmerich 2015

• Bounded Archiver using Lebesgue Measure Knowles, Corne, Fleischer 2003
• SMS-EMOA
  • original conference publication Emmerich, Beume, and Naujoks 2005
  • extended journal publication, see Nicola Beume, Boris Naujoks, Michael Emmerich, 2007
  • efficient implementation with efficient incremental updates (O(log n) amortized time per iteration in 2-D and O(n) in 3-D), see Hupkens and Emmerich, 2013
  • Parallel SMS EMOA for Many Objective Optimization Goméz, Coello Coello, and Alba

• HypE
  • see Johannes Bader and Eckart Zitzler. HypE: An Algorithm for Fast Hypervolume-Based Many-Objective Optimization. Evolutionary Computation, posted online since July 22, 2010
  • code available on the PISA web page

• MO-CMA-ES
  • see Christian Igel, Nikolaus Hansen, Stefan Roth, 2007
  • code available within the Shark library

• POSEA - Portfolio-based Selection based on Hypervolume (POSEA)
  • Algorithm description and empirical performance assessment Guerreiro, Yevseyeva, Emmerich, and Fonseca 2014
  • Hypervolume based Sharpe Indicator, theoretical results Fonseca and Guerreiro, 2016

• Efficient Global Optimization
  • Early ideas on infill criteria based on hypervolume, see http://link.springer.com/chapter/10.1007/978-3-642-15844-5_72
  • Efficient Multicritera Optimization with extensive benchmark Couckuyt, Deschrijver, and Dhaene 575
  • Efficient Multicritera Optimization, efficient implementation (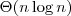) Emmerich, Yang, Wang, and Fonseca 2016

• Hypervolume-based Newton's Method Sosa Hernandéz, Schütze, and Emmerich (2014)

• Water Distribution Network Design
  • Edgar Reehuis, Johannes Kruisselbrink, Andre Deutz, Thomas Baeck, Michael Emmerich, Multiobjective optimization of water distribution networks using SMS-EMOA, EUROGEN 2011, C. Poloni, D. Quagliarella, J. Periaux, N. Gauger and K. Giannakoglou (Eds.), CIRA, Capua, Italy 2011, pages 269-279
• Grid Computing
  • Kuijl, A. v. d., Emmerich, M. T. M. and Li, H. (2010), A robust multi-objective resource allocation scheme incorporating uncertainty and service differentiation. Concurrency and Computation: Practice and Experience, 22: 314–328. doi: 10.1002/cpe.1481
• Software Architecture Design
  • Rui Li, R. Etemaadi, Michael T. M. Emmerich, and Michel R. V. Chaudron. An Evolutionary Multiobjective Optimization Approach to Component-Based Software Architecture Design. IEEE Conference on Evolutionary Computation, New Orleans, June 5-8, 2011.
• Molecular Control
  • J.W. Klinkenberg, T.M. Emmerich, A.H. Deutz, O.M. Shir, T. Baeck: A reduced-cost SMS-EMOA using kriging, self-adaptation, and parallelization In M. Ehrgott et al.: Conference on Multicriteria Decision Making 2008, January 2008, Auckland, NZ , Lecture Notes on Economy and Mathematical Systems, 2009 Springer
• Planning Software
  • Hui Li, Giuliano Casale, and Tariq Ellahi. 2010. SLA-driven planning and optimization of enterprise applications. In Proceedings of the first joint WOSP/SIPEW international conference on Performance engineering (WOSP/SIPEW '10). ACM, New York, NY, USA, 117-128.
• Airfoil Optimization
  • Boris Naujoks, Nicola Beume, and Michael Emmerich. Metamodel-Assisted SMS EMOA Applied to Airfoil Optimization Tasks. In R. Schilling, W. Haase, J. Periaux, and H. Baier, editors, Proceedings EUROGEN'05 (CD-ROM). FLM, TU Munich, 2005

• Docking Problems in Drug Discovery, in Sanchez{-}Faddeev, Emmerich Verbeek, Henry, Grimshaw, Spaink, van Vlijmen and Bender

• Bioplant-Controller Design Yang, Gaida, Bäck, Emmerich

• A review paper on the hypervolume indicator in multiobjective optimization Auger, Bader, Brockhoff and Zitzler 2012

• Set-oriented and Indicator Based Optimization: Open Theoretical Problem Page (includes recent results and open questions on the hypervolume indicator and related measures), see Emmerich, Naujoks, Brockhoff 2013-