Evolutionäre Algorithmen

Seit etwa 4 Milliarden Jahren gibt es Leben auf unserer Erde. Neben der erstaunlichen Artenvielfalt hat die Evolution auch viele Organismen und Formen hervorgebracht, die gut und zum Teil optimal an ihre jeweilige Umwelt angepasst sind. Warum sollte man nicht versuchen, durch die Nachahmung von grundlegenden Evolutionsprinzipien zu neuen, robusteren Optimierverfahren zu kommen?

Anfang der sechziger Jahre stellten sich verschiedene Forscher unabhängig voneinander diese Frage. In Deutschland führte dies zu den Evolutionsstrategien (ES), in den USA zu den genetischen Algorithmen (GA) und zum Konzept des evolutionary programming (EP). Diese Verfahren sowie das später hinzugekommene genetic programming (GP), das evolutionäre Suchprinzipien in den Suchraum von Programmiersprachen überträgt, werden heute unter dem Namen evolutionäre Algorithmen (EA) bzw. evolutionary computation (EC) zusammengefasst. Die verschiedenen Klassen evolutionärer Algorithmen unterscheiden sich durch die Repräsentation der Individuen und demzufolge auch durch die auf ihr arbeitenden genetischen Operatoren. Ein wichtiger Vorteil aller evolutionärer Verfahren ist ihre inhärente, skalierbare Parallelität. Auf diese Weise kann die Rechenleistung beliebiger Parallelrechnerarchitekturen für rechenintensive Probleme genutzt werden.

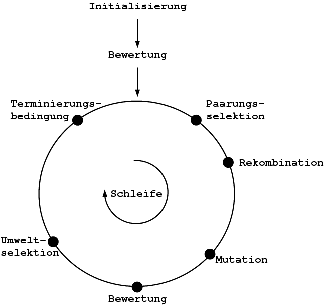
Eine Menge von Individuen bildet die Population, die sich unter Verwendung folgender (sog. genetischer) Operatoren verändert: Die Mutation ist ein stochastischer Operator, der die genetische Information eines Individuums modifiziert, nachdem die Rekombination nur genetisches Material der Eltern neu zu einem Nachkommen zusammengesetzt hat. Die Selektion bestimmt, welche Individuen in der nächsten Generation zur Fortpflanzung zugelassen werden.

Obwohl ursprünglich für die experimentelle Optimierung und diskrete Suchräume entwickelt, bilden die reellen Zahlen seit der Realisierung auf Rechnern typischerweise den Suchraum von Evolutionsstrategien. Für diesen Fall ist die Theorie der ES am weitesten fortgeschritten. Daher besteht ein Individuum aus einem n-dimensionalen reellwertigen Objektvariablenvektor und einer Menge von Strategieparametern, welche die Mutation steuern. Die Anzahl der Strategieparameter kann je nach Einstellung zwischen 1 und n + n(n - 1)/2 variieren.

Die Besonderheit von ES liegt darin begründet, dass sowohl Objekt- als auch Strategieparameter rekombiniert und mutiert werden, wodurch sich bei entsprechender Selektion die Möglichkeit einer ständigen Selbstadaptation der Suchschrittweiten und ggf. auch der Vorzugsrichtungen ergibt. Wesentlich für das Gelingen der Selbstanpassung ist ein Geburtenüberschuss, der durch Selektion wieder abgebaut wird. Untersucht werden Konvergenzeigenschaften, der Einfluss verschiedener Operatoren und Erweiterungen des Grundalgorithmus auf die mehrfache Zielsetzung, dynamische Optimierung und verschiedene Parallelisierungsansätze.

In GA werden typischerweise Bitstrings zur Repräsentation von Individuen verwendet. Dies bedeutet jedoch nicht, dass man mit GA nur pseudo-Boolesche Probleme angehen kann, für die diese Kodierung direkt geeignet ist. Komplexere Datenstrukturen wie reelle Zahlen, Listen, Bäume etc. müssen in geeigneter Weise auf Bitstrings abgebildet werden. Allerdings schwächt jede zusätzliche Abbildung zwischen der binären und der Problemrepräsentation die nötige Kausalität zwischen Geno- und Phänotyp, so dass im Einzelfall zu überlegen ist, ob man nicht eine für das Problem generische Repräsentation wählt und die genetischen Operatoren anpasst, anstatt einen Standard-GA zu verwenden und die Entscheidungsvariablen mehr oder weniger geschickt in einem Bitstring zu kodieren.

Die Partnerselektion wählt zwei Individuen aus der Population für die nächste Paarung mit einer zu ihrer Fitness proportionalen Wahrscheinlichkeit aus. Der Nachkomme übernimmt Gene von beiden Elternteilen. Anschließend werden mit einer geringen Wahrscheinlichkeit die Bits mutiert (invertiert). Die so erzeugten Nachkommen ersetzen die Elternpopulation. Dieses Vorgehen wird wiederholt, bis ein Terminierungskriterium greift.

Genetisches Programmieren (GP) bezeichnet eine Menge von evolutionären Verfahren, die Computerprogramme generieren, welche Algorithmen repräsentieren, die zur Lösung eines bestimmten Problems dienen. Die Problemlösungsfähigkeit (Fitness) derartiger Genotypen ist bestimmt durch die Fähigkeit des von ihm repräsentierten Algorithmus, eine problemspezifische Input-Output-Relation bestmöglich zu approximieren. GP-Verfahren sind in vielen Problemdomänen praktisch einsetzbar, z.B. Datenanalyse, Steuer- und Regelungstechnik, Ökonomie, Robotik oder Sozionik.

In Abhängigkeit von der Repräsentation der Individuen unterscheidet man mittlerweile eine ganze Reihe verschiedener GP-Varianten. In der traditionellen Form werden die Programme als Syntaxbäume einer funktionalen Programmiersprache repräsentiert. Eine andere etablierte Variante, lineares GP, verwendet stattdessen imperativen Programmcode. Letztere schließt auch die Evolution von Maschinenprogrammen ein. Beim AIMGP-Verfahren (Automatic Induction of Machine Code with Genetic Programming) werden die Programme direkt als binärer Maschinenkode ausgeführt, ohne vorher eine Interpretation zu durchlaufen. Auf diese Weise wird dieser zeitkritische Schritt der genetischen Programmierung erheblich beschleunigt. Eine weitere Möglichkeit, die Ausführungzeit der Programme zu reduzieren, besteht darin, den für das lineare GP typischen nicht-effektiven Kode aus den Programmen zu entfernen, bevor deren Fitness bestimmt wird. Andere GP-Ansätze betrachten Programmgraphen oder kombinieren verschiedene Repräsentationsformen in einem Individuum. In diesem Zusammenhang haben sich insbesondere Verzweigungsgraphen von linearen Programmsequenzen (sogenannte lineare Graphen) bewährt.