


Next: Bibliography
Final Report for the GK "Materials and Concepts of Quantum Information Processing"
Ralf Stadelhofer
GK-Scholarship Holder: 01.11.2001 - 31.10.2004
e-mail: ralf.stadelhofer@udo.edu
University of Dortmund
Department of Computer Science
Date: November 18, 2004
The concept of computational power provides a fundamental new language for studying the relationship between classical and
quantum physics. Unfortunately the development of quantum algorithms (QA) is a very cumbersome task due to the
counterintuitive character of quantum physics. The approach we use in our work to develop QAs is the usage of an automatic
algorithm design technique called Genetic Programming (GP). The usage of GP in evolving quantum algorithms was
pioneered by [4,10].
In GP one evolves algorithms by imitating nature in
the evolution of species. In our work this imitation proceeds as follows:
- Each individual of a population is a QA which itself is described by an unitary operation. As any unitary operation can
be decomposed into a sequence of one- and two-qubit gates (elementary quantum gates) one can represent a quantum algorithm
by such a sequence. Thus each individual (QA) of a population is a sequence of elementary quantum gates.
- To detect how well an individual of a population in the GP system solves a problem, one can simulate the corresponding quantum
algorithm on a classical computer. The measurement probabilities thus obtained are used to calculate a
fitness value that indicates the ability of the quantum algorithm to solve the posed problem.
- Dependent on this fitness value, new individuals are created by mutations and crossover.
- Promising individuals are produced by repeating this procedure of fitness calculations, mutations and crossovers, several times.
The fitness calculation of a QA cannot be done efficiently on a classical computer because quantum gates are represented by unitary
matrices whose dimension grows exponentially with the number of qubits. As a whole population of up to 5000 QAs has to be evaluated
in each generation (up to 5000 generations) one is
limited to a small number of qubits (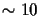 ) to keep the time, such a simulation takes, in reasonable limits. This limitation
forced us to: a) introduce a new kind of oracle gates, and b) to restrict the class of problems to decision problems:
) to keep the time, such a simulation takes, in reasonable limits. This limitation
forced us to: a) introduce a new kind of oracle gates, and b) to restrict the class of problems to decision problems:
- a)
- An oracle gate O is used to encode the value
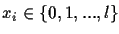 with
with
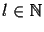 that is
returned by a black-box
that is
returned by a black-box
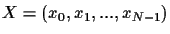 on input
on input
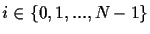 ,
into the quantum system. Usually this is done using two quantum registers, one carrying the index
,
into the quantum system. Usually this is done using two quantum registers, one carrying the index
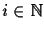 of the
black-box element to be queried and another to store the output
of the
black-box element to be queried and another to store the output 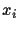 of such a query:
of such a query:
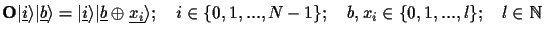 |
(1) |
Here and in what follows we use
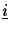 ,
,
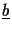 and
and
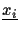 to denote the binary decomposition of the integers
to denote the binary decomposition of the integers
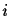 ,
, 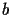 and
and 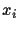 , respectively.
, respectively.
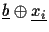 denotes the bitwise XOR operation between the
bit strings
denotes the bitwise XOR operation between the
bit strings
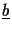 and
and
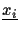 .
This scheme is a straightforward way to ensure that the oracle gate is unitary. Unfortunately one needs an extra output register
of
.
This scheme is a straightforward way to ensure that the oracle gate is unitary. Unfortunately one needs an extra output register
of
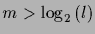 qubits which increases the time necessary to simulate the quantum algorithm on a classical computer
exponential in
qubits which increases the time necessary to simulate the quantum algorithm on a classical computer
exponential in 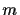 . Therefore it is reasonable, as proposed by [6], to test oracle gates that encode the black-box entries
. Therefore it is reasonable, as proposed by [6], to test oracle gates that encode the black-box entries 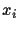 into
phase shifts of the query register
into
phase shifts of the query register
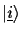 :
:
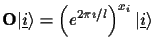 |
(2) |
Sometimes it is helpful to use a hybrid approach that encodes the value 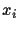 partly into a phase shift of the query
register and partly into an output register:
partly into a phase shift of the query
register and partly into an output register:
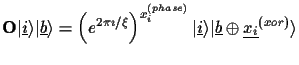 |
(3) |
Here we used a decomposition of the integer 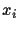 into the integer
into the integer
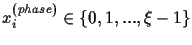 and into the binary string
and into the binary string
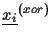 . Consider for example the integer
. Consider for example the integer
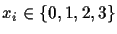 which is to be encoded into
a quantum state that only has one output qubit. As
which is to be encoded into
a quantum state that only has one output qubit. As 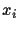 can be encoded unambiguously into two bits one has
to encode one of these two bits into the output register and the other by a phase shift. For
can be encoded unambiguously into two bits one has
to encode one of these two bits into the output register and the other by a phase shift. For
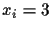 one gets:
one gets:
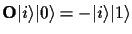 .
All the oracle gates presented here are valid quantum operations and can be easily implemented in an experiment.
.
All the oracle gates presented here are valid quantum operations and can be easily implemented in an experiment.
- b)
- In a decision problem one wants to know if a black-box has a certain property (as periodicity) or not.
The restriction on decision problems is due to the fact that otherwise we would need an extra readout register to store the
numerical result of a computation. Also this restriction makes it possible to introduce a GP-system that can find the most
convenient measurement procedure by its own. Such a measurement procedure can reduce the necessity of extra qubits needed
for post computations that allow an encoding of the answer into a single output qubit.
Using the guidelines mentioned above we were able to develop the following scalable and formerly unknown QAs:
- 1)
- Quantum algorithms solving the parity problem on single issue and ensemble quantum computers:
The determination of the parity of a string of 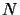 binary digits
is a well known problem in classical as well as in quantum information processing,
which can be formulated as a black-box problem.
It has been established that quantum algorithms require at least
binary digits
is a well known problem in classical as well as in quantum information processing,
which can be formulated as a black-box problem.
It has been established that quantum algorithms require at least 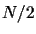 oracle calls [1,2].
In [9] we present an algorithm, developed using GP, that reaches this lower bound and is also optimal in terms
of additional gate operations required.
There we also discuss its application to pure and mixed states.
Since it can be applied directly to thermal states,
it does not suffer from signal loss associated with pseudo-pure state preparation.
We also show that for ensemble quantum computers the number of oracle calls can be further reduced
by a factor
oracle calls [1,2].
In [9] we present an algorithm, developed using GP, that reaches this lower bound and is also optimal in terms
of additional gate operations required.
There we also discuss its application to pure and mixed states.
Since it can be applied directly to thermal states,
it does not suffer from signal loss associated with pseudo-pure state preparation.
We also show that for ensemble quantum computers the number of oracle calls can be further reduced
by a factor 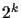 , provided the signal to noise ratio is sufficiently high.
This additional speedup is linked to (classical) parallelism
of the ensemble quantum computer.
In [9] we also demonstrate the experimental realizations of the parity algorithms on a liquid-state NMR quantum
computer.
, provided the signal to noise ratio is sufficiently high.
This additional speedup is linked to (classical) parallelism
of the ensemble quantum computer.
In [9] we also demonstrate the experimental realizations of the parity algorithms on a liquid-state NMR quantum
computer.
- 2)
- An exact and scalable quantum algorithm solving a special case of the hidden subgroup problem:
Simon's problem [5] was the first one that showed an
exponential gap in the number of oracle queries needed by a quantum algorithm and those needed by any classical probabilistic
algorithm. Simon's problem can be stated as a hidden subgroup problem and the algorithm solving it is a
probabilistic one. Therefore it is suggestive to explore the conditions under which related problems can be solved
by an exact algorithm.
With the help of our GP system it was possible to develop a formerly unknown exact and scalable quantum algorithm that
solves the following special case of the hidden subgroup problem:
Here we demanded the group 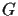 to be
to be
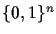 with the bitwise XOR operation as group multiplication. If one drops
these two restrictions the above problem is the general hidden subgroup problem. Also we used the notation
with the bitwise XOR operation as group multiplication. If one drops
these two restrictions the above problem is the general hidden subgroup problem. Also we used the notation 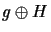 to
denote the coset of
to
denote the coset of 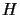 : If the group
: If the group 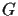 has the subgroup
has the subgroup
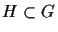 then to each
then to each 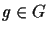 one can define a set
one can define a set
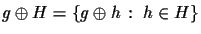 which is also called a coset of
which is also called a coset of 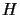 .
.
Our quantum algorithm solves this problem with two oracle calls, only. The upper part of figure 1
shows this algorithm on three qubits, the lower part shows this algorithm on four qubits. Because
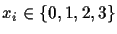 one can decompose
one can decompose 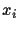 into two binary values
into two binary values
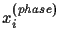 and
and
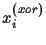 .
Using this property
our oracle gate
.
Using this property
our oracle gate 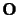 is defined analogous to Eq. (3) by
is defined analogous to Eq. (3) by
Measurement of the final state returns the state
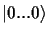 if
if 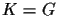 , otherwise one does not measure
, otherwise one does not measure
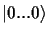 .
.
An exact classical algorithm that solves this problem needs at
most 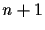 black-box queries (here:
black-box queries (here:
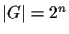 ) where
) where 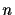 denotes the number of query qubits. A probabilistic classical
algorithm can solve this problem using
denotes the number of query qubits. A probabilistic classical
algorithm can solve this problem using 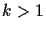 queries with an error probability of
queries with an error probability of 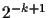 (for
(for
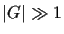 ).
).
Figure:
Quantum algorithms on three and four qubits as found by our GP system. The lowest qubit is an ancillary
qubit and corresponds to the binary variable b in the
definition of  :
:
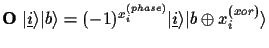 .
The upper
.
The upper  query qubits are used to encode
query qubits are used to encode
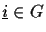 .
H denotes the Hadamard gate and
.
H denotes the Hadamard gate and
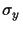 denotes
a Pauli matrix.
denotes
a Pauli matrix.
|
|
Despite the algorithms presented above we were also able to develop a quantum algorithm that solves a special case of
the Deutsch-Jozsa problem [8]. But, as we noticed, this algorithm was already discovered in [7],
therefore we didn't present this algorithm here.
Up to this work, as far as we know, all quantum algorithms found with the help of GP were either already known quantum algorithms
[4], unknown but not scalable
quantum algorithms [11] or scalable quantum algorithms that do not show any quantum speedup [4]. Using
GP we were able to evolve scalable, formerly unknown better-than-classical quantum algorithms, which indicates that
automated programming techniques provide a useful and not yet fully explored tool in the quest for new quantum algorithms.



Next: Bibliography
Ralf Stadelhofer
2004-11-18
![]() one can decompose
one can decompose ![]() into two binary values
into two binary values
![]() and
and
![]() .
Using this property
our oracle gate
.
Using this property
our oracle gate ![]() is defined analogous to Eq. (3) by
is defined analogous to Eq. (3) by
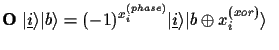 with
with![]() black-box queries (here:
black-box queries (here:
![]() ) where
) where ![]() denotes the number of query qubits. A probabilistic classical
algorithm can solve this problem using
denotes the number of query qubits. A probabilistic classical
algorithm can solve this problem using ![]() queries with an error probability of
queries with an error probability of ![]() (for
(for
![]() ).
).